题目内容
若x4(x+3)8=a0+a1(x+2)+a2(x+2)2+…+a12(x+2)12,则log2(a1+a3+a5+…+a11)=( )
A.27 B.28 C.7 D.8
C
[解析] 取x=-1,得
(-1)4(-1+3)8=a0+a1+a2+…+a11+a12,①
取x=-3,得
(-3)4(-3+3)8=a0-a1+a2-…-a11+a12,②
①与②两式左、右两边分别相减,得
28=2(a1+a3+a5+…+a11),
所以a1+a3+a5+…+a11=27,
所以log2(a1+a3+a5+a7+a9+a11)=log227=7.

练习册系列答案
相关题目
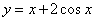 在区间
在区间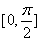 上的最大值是 . .
上的最大值是 . .  则
则 的最大值是________.
的最大值是________. 表示区域为D,且圆x2+y2=4在D内的弧长为
表示区域为D,且圆x2+y2=4在D内的弧长为 ,则实数a的值等于________.
,则实数a的值等于________.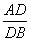 =
=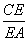 =
=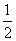 (如图①).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C(如图②).
(如图①).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C(如图②).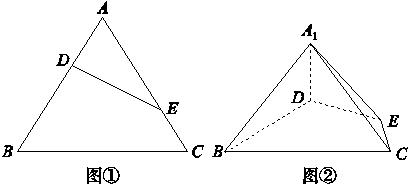
 的性质,有如下说法:①函数f(x)的最小值为3;②函数f(x)为偶函数;③函数f(x)的单调递增区间为(-∞,0].
的性质,有如下说法:①函数f(x)的最小值为3;②函数f(x)为偶函数;③函数f(x)的单调递增区间为(-∞,0].