题目内容
在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:
(1)对任意a∈R,a*0=a;
(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).
关于函数f(x)=(ex)* 的性质,有如下说法:①函数f(x)的最小值为3;②函数f(x)为偶函数;③函数f(x)的单调递增区间为(-∞,0].
的性质,有如下说法:①函数f(x)的最小值为3;②函数f(x)为偶函数;③函数f(x)的单调递增区间为(-∞,0].
其中所有正确说法的个数为( )
A.0 B.1
C.2 D.3
C
[解析] 由题意可知,f(x)=(ex)* =ex·
=ex· +ex+
+ex+ =ex+
=ex+ +1.
+1.
所以ex+ ≥2
≥2 =2,故f(x)≥2+1=3,当且仅当x=0时“=”成立,知①正确;
=2,故f(x)≥2+1=3,当且仅当x=0时“=”成立,知①正确;
由f(-x)=e-x+ +1=ex+
+1=ex+ +1=f(x),故f(x)是偶函数,知②正确;
+1=f(x),故f(x)是偶函数,知②正确;
由f′(x)= =ex-
=ex- =
= ,令f′(x)>0,即e2x-1>0,故x>0,知③不正确.综上,知选C.
,令f′(x)>0,即e2x-1>0,故x>0,知③不正确.综上,知选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

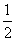 x+a,则函数f(x)的零点个数是( )
x+a,则函数f(x)的零点个数是( )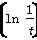 ≤2f(1),那么t的取值范围是________.
≤2f(1),那么t的取值范围是________. 若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是( )
若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是( ) ,+∞) B.
,+∞) B.
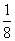 y2的焦点为F(m,0),点M的坐标为(-m,m),过C的焦点且斜率为k的直线与C交于A,B两点.若
y2的焦点为F(m,0),点M的坐标为(-m,m),过C的焦点且斜率为k的直线与C交于A,B两点.若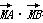 =0,则k=( )
=0,则k=( )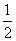 B.
B.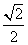 C.
C.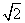 D.2
D.2