题目内容
19．若（2x-1）2016=a0+a1x+…+a2016x2016（x∈R），则$\frac{1}{2}$+$\frac{{a}_{2}}{{2}^{2}{a}_{1}}$+$\frac{{a}_{3}}{{2}^{3}{a}_{1}}$+…+$\frac{{a}_{2016}}{{2}^{2016}{a}_{1}}$=（ ）| A． | -$\frac{1}{2015}$ | B． | $\frac{1}{2016}$ | C． | -$\frac{1}{4030}$ | D． | $\frac{1}{4032}$ |
分析 根据二项式定理可得a1=-2×2016，a0=1．在已知等式中令x=$\frac{1}{2}$，可得a0+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2016}}{{2}^{2016}}$=0，$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2016}}{{2}^{2016}}$=2015，即可得出．
解答 解：根据二项式定理可得a1=-2×2016，a0=1．
在已知等式中令x=$\frac{1}{2}$，可得a0+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2016}}{{2}^{2016}}$=0，
∴$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2016}}{{2}^{2016}}$=2015，
∴$\frac{1}{2}$+$\frac{{a}_{2}}{{2}^{2}{a}_{1}}$+$\frac{{a}_{3}}{{2}^{3}{a}_{1}}$+…+$\frac{{a}_{2016}}{{2}^{2016}{a}_{1}}$=$\frac{1}{2}$-$\frac{1}{2×2016}$×2015=$\frac{2016-2015}{4032}$=$\frac{1}{4032}$，
故选：D．
点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
4．当1＜m＜$\frac{3}{2}$时，复数（3+i）-m（2+i）在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
11．命题“若a2＜b，则-$\sqrt{b}$＜a＜$\sqrt{b}$”的逆否命题为（ ）
| A． | 若a2≥b，则a≥$\sqrt{b}$或a≤-$\sqrt{b}$ | B． | 若a2≥b，则a＞$\sqrt{b}$或a＜-$\sqrt{b}$ | ||
| C． | 若a≥$\sqrt{b}$或a≤-$\sqrt{b}$，则a2≥b | D． | 若a＞$\sqrt{b}$或a＜-$\sqrt{b}$，则a2≥b |
8．设Sn是等差数列{an}的前n项和，且满足等式S7=a5+a6+a8+a9，则$\frac{{a}_{7}}{{a}_{4}}$的值为（ ）
| A． | $\frac{7}{4}$ | B． | $\frac{4}{7}$ | C． | $\frac{7}{8}$ | D． | $\frac{8}{7}$ |
9．
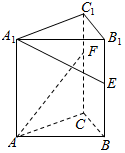如图，在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6，若E，F分别是棱BB1，CC1上的点，且BE=B1E，C1F=$\frac{1}{3}$CC1，则异面直线A1E与AF所成角的余弦值为（ ）
如图，在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6，若E，F分别是棱BB1，CC1上的点，且BE=B1E，C1F=$\frac{1}{3}$CC1，则异面直线A1E与AF所成角的余弦值为（ ）| A． | $\frac{\sqrt{3}}{6}$ | B． | $\frac{\sqrt{2}}{6}$ | C． | $\frac{\sqrt{3}}{10}$ | D． | $\frac{\sqrt{2}}{10}$ |