题目内容
(本小题满分l4分)已知数列 的前n项和为
的前n项和为 ,正数数列
,正数数列 中
中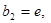
(e为自然对数的底 )且
)且 总有
总有 是
是 与
与 的等差中项,
的等差中项, 的等比中项.
的等比中项.
(1) 求证: 有
有 ;
;
(2) 求证: 有
有 .
.
 的前n项和为
的前n项和为 ,正数数列
,正数数列 中
中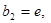
(e为自然对数的底
 )且
)且 总有
总有 是
是 与
与 的等差中项,
的等差中项, 的等比中项.
的等比中项.(1) 求证:
 有
有 ;
; (2) 求证:
 有
有 .
.解:(1)  是
是 与
与 的等差中项
的等差中项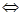

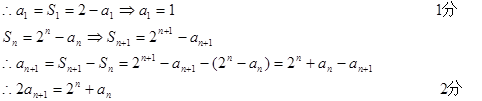
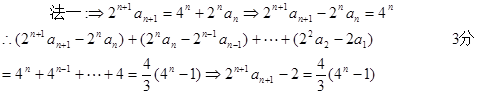

(2)由(1)得
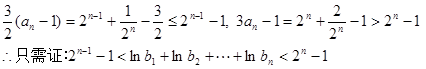
 6分
6分
 的等比中项
的等比中项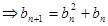
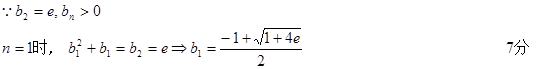
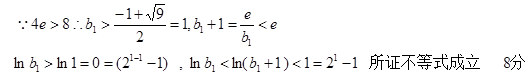
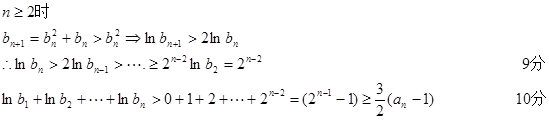
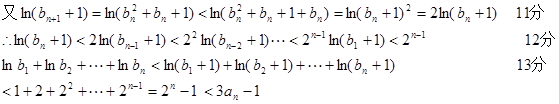
综上所述,总有 成立 14分
成立 14分
解法二:

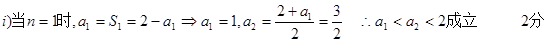
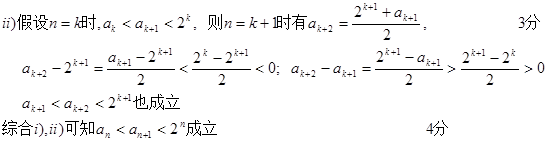
(2)
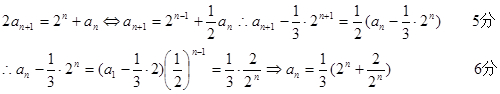
 的等比中项
的等比中项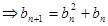
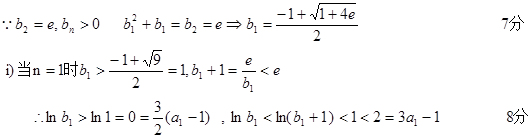
ii)假设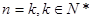 时不等式
时不等式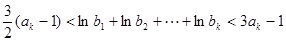 成立,
成立,
则n=k+1时要证明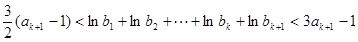
只需证明: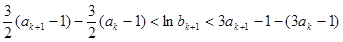
即只需证明: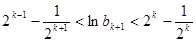 ….9分
….9分
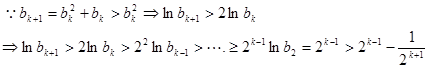 ……..10分
……..10分
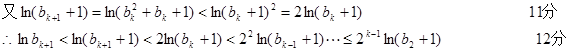 只需证明
只需证明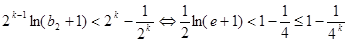
只需证明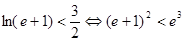 13分
13分
由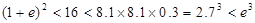 可知上面结论都成立
可知上面结论都成立
综合(i)(ii)可知 ,
,  成立 …..14分
成立 …..14分
法三:
n=1时同法一: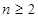 时左边证明同法一 10分
时左边证明同法一 10分
当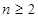 时,证明右边如下:
时,证明右边如下:
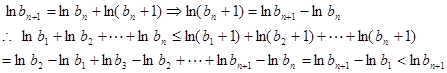
只需证明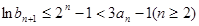 11分
11分
 只需证明
只需证明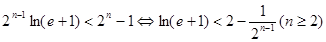
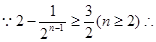 只需证明
只需证明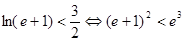 13分
13分
由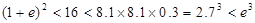 可知上面结论都成立
可知上面结论都成立
综上所述 ,
,  成立 …..14分
成立 …..14分
注1: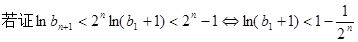 必须
必须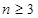 才行
才行
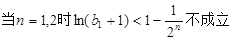
实际上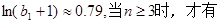
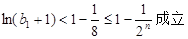
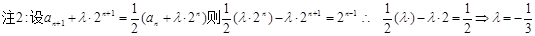
 是
是 与
与 的等差中项
的等差中项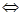

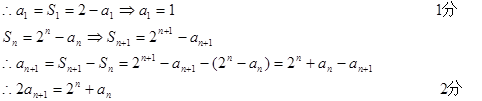
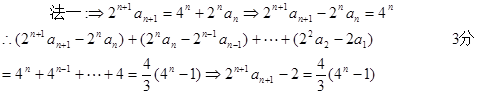

(2)由(1)得

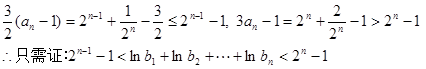
 6分
6分 的等比中项
的等比中项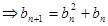
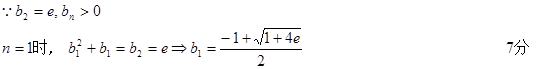
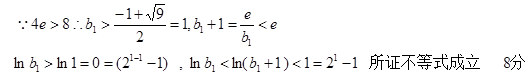
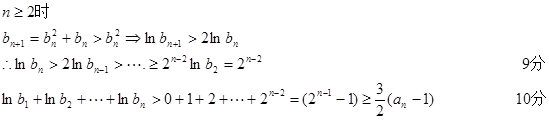
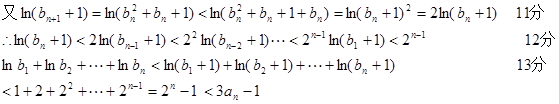
综上所述,总有
 成立 14分
成立 14分解法二:

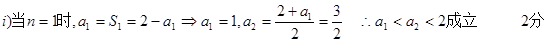
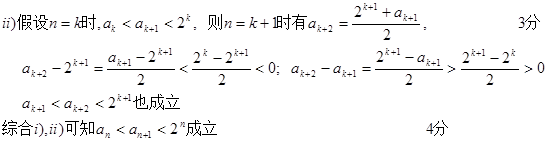
(2)
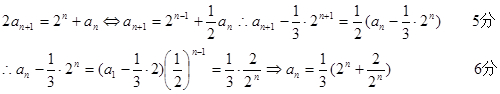
 的等比中项
的等比中项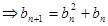
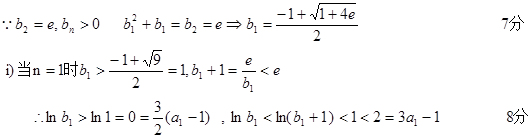
ii)假设
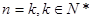 时不等式
时不等式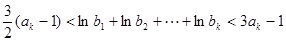 成立,
成立, 则n=k+1时要证明
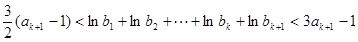
只需证明:
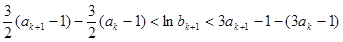
即只需证明:
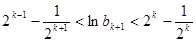 ….9分
….9分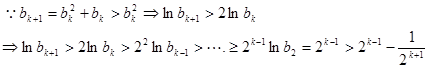 ……..10分
……..10分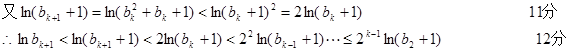 只需证明
只需证明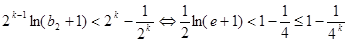
只需证明
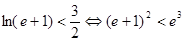 13分
13分由
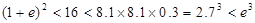 可知上面结论都成立
可知上面结论都成立 综合(i)(ii)可知
 ,
,  成立 …..14分
成立 …..14分法三:
n=1时同法一:
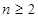 时左边证明同法一 10分
时左边证明同法一 10分当
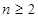 时,证明右边如下:
时,证明右边如下: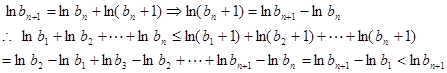
只需证明
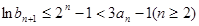 11分
11分 只需证明
只需证明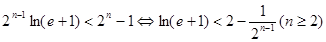
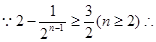 只需证明
只需证明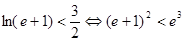 13分
13分由
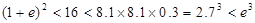 可知上面结论都成立
可知上面结论都成立 综上所述
 ,
,  成立 …..14分
成立 …..14分注1:
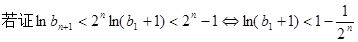 必须
必须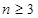 才行
才行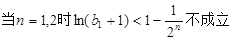
实际上
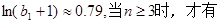
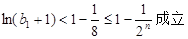
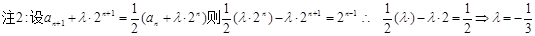
略

练习册系列答案
相关题目
 ,将函数
,将函数 的所有极值点从小到大排成一数列,记为
的所有极值点从小到大排成一数列,记为
 的通项公式;
的通项公式; ,求数列
,求数列 前n项和
前n项和
 中,
中, ,
, ,且
,且 .
.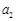 及
及 是
是 ,使
,使 成等比数列?如存在,试分别写出
成等比数列?如存在,试分别写出 和
和 关于
关于 的一个表达式,并给出证明;
的一个表达式,并给出证明;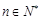 ,
, .
. 1)小问6分,(2)小分6分.)
1)小问6分,(2)小分6分.)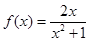 ,数列
,数列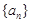 满足
满足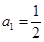 ,
,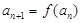 ,
,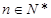 .
.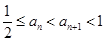 ;
;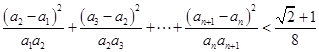 .
. 中,
中,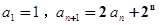
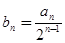 ,证明:数列
,证明:数列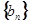 是等差数列。
是等差数列。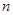 项和
项和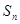 。
。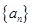 的前
的前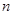 项和为
项和为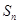 ,对任意的正整数
,对任意的正整数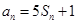 成立,记
成立,记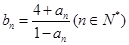 ?
?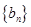 的通项公式;
的通项公式;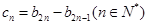 ,设数列
,设数列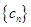 的前
的前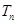 ,求证:对任意正整数
,求证:对任意正整数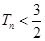 ;
;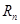 ?已知正实数
?已知正实数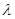 满足:对任意正整数
满足:对任意正整数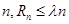 恒成立,求
恒成立,求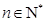 ,圆
,圆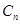 :
: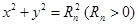 与
与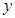 轴正半轴的交点为
轴正半轴的交点为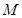 ,与曲线
,与曲线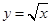 的交点为
的交点为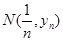 ,直线
,直线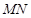 与
与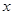 轴的交点为
轴的交点为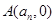 .
.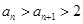 ;
;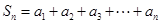 ,
,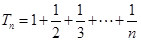 ,求证:
,求证: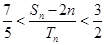 .
.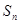 是数列
是数列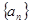 的前
的前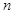 项和,
项和,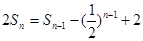 (
(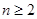 ,
,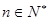 ),且
),且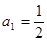 .
.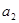 的值,并写出
的值,并写出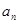 和
和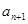 的关系式;
的关系式; 3)我们可以证明:若数列
3)我们可以证明:若数列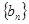 有上界(即存在常数
有上界(即存在常数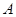 ,使得
,使得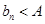 对一切
对一切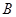 ,使得
,使得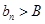 对一切
对一切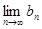 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: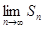 存在.
存在.  下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)

 为表1中第n行各个数字之和,求
为表1中第n行各个数字之和,求
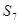 ,并归纳出
,并归纳出