题目内容
已知向量a=(cos 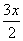 ,sin
,sin 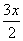 ),b=(cos
),b=(cos  ,-sin
,-sin  ),且x∈
),且x∈ .
.
(1)求a·b及|a+b|;
(2)若f(x)=a·b-|a+b|,求f(x)的最大值和最小值.
解 (1)a·b=cos 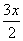 cos
cos  -sin
-sin 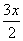 sin
sin  =cos 2x,
=cos 2x,
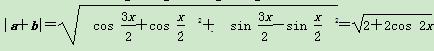 =2|cos x|,
=2|cos x|,
∵x∈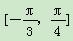 ,∴cos x>0,
,∴cos x>0,
∴|a+b|=2cos x.
(2)f(x)=cos 2x-2cos x=2cos2x-2cos x-1=2(cos x- )2-
)2-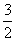 .
.
∵x∈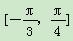 .∴
.∴ ≤cos x≤1,
≤cos x≤1,
∴当cos x= 时,f(x)取得最小值-
时,f(x)取得最小值-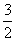 ;当cos x=1时,f(x)取得最大值-1.
;当cos x=1时,f(x)取得最大值-1.

练习册系列答案
相关题目
 )的部分图象,如图所示.
)的部分图象,如图所示.
 上有两个不同的实根,试求a的取值范围.
上有两个不同的实根,试求a的取值范围.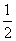 ),n=(
),n=( ,0),点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动.且满足
,0),点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动.且满足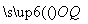 =m⊗
=m⊗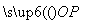 +n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别为( )
+n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别为( ) )+asin(x-
)+asin(x-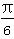 )的一条对称轴方程为x=
)的一条对称轴方程为x= ,则a等于( )
,则a等于( )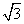 C.2 D.3
C.2 D.3 有且只有一个零点的充分必要条件是________.
有且只有一个零点的充分必要条件是________. ,x∈(0,3),则( )
,x∈(0,3),则( ) B.f(x)有最小值-1
B.f(x)有最小值-1