题目内容
若定义在R上的奇函数y=f（x），满足f（x+1）=f（1-x），则周期为 ．
考点：函数的周期性
专题：函数的性质及应用
分析：在给出的等式中以x+1替换x，借助于函数是奇函数求得函数的周期．
解答：
解：由f（x+1）=f（1-x），且f（x）为奇函数，得
f（x+1+1）=f（1-x-1）=f（-x）=-f（x），
即f（x+2）=-f（x），
则f（x+4）=-f（x+2）=-[-f（x）]=f（x）．
∴f（x）的周期为4．
故答案为：4．
f（x+1+1）=f（1-x-1）=f（-x）=-f（x），
即f（x+2）=-f（x），
则f（x+4）=-f（x+2）=-[-f（x）]=f（x）．
∴f（x）的周期为4．
故答案为：4．
点评：本题考查了函数奇偶性的性质，是基础题．
练习册系列答案
互动英语系列答案
相关题目
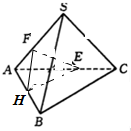如图，一个四面体S-ABC的六条棱长都为4，E为SA的中点，过点E作平面EFH∥平面SBC．且平面EFH∩平面ABC=FH，则△HFE面积为动点P到x轴，y轴的距离之比等于非零常数k，则动点P的轨迹方程是（ ）
A、y=
| ||
| B、y=kx（x≠0） | ||
C、y=-
| ||
| D、y=±kx（x≠0） |
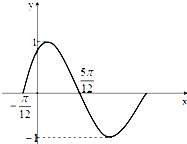函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，φ＜