题目内容

F1、F2是椭圆
x2
16
+
y2
3
=1的两个焦点，P是椭圆上一点，则|PF1|•|PF2|有最
 
值为
 
．
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：运用椭圆的定义，可得|PF1|+|PF2|=2a=8，再由基本不等式，即可求得|PF1|•|PF2|的最大值．
解答： 解：椭圆
x2
16
+
y2
3
=1的a=4，
则|PF1|+|PF2|=2a=8，
则|PF1|•|PF2|≤（
|PF1|+|PF2|
2
）2=16，
当且仅当|PF1|=|PF2|=4，
则|PF1|•|PF2|有最大值，且为16．
故答案为：大，16
点评：本题考查椭圆的定义和性质，考查基本不等式的运用：求最值，考查运算能力，属于基础题．
练习册系列答案
相关题目
若sinx＜0且cosx＞0则角x所在的象限是第
 
象限．（只填数字）
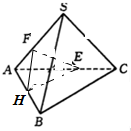如图，一个四面体S-ABC的六条棱长都为4，E为SA的中点，过点E作平面EFH∥平面SBC．且平面EFH∩平面ABC=FH，则△HFE面积为
 
．
已知函数f（x）=
a
a2-1
（ax-a-x），其中a＞0，a≠1
（1）写出f（x）的奇偶性与单调性（不要求证明）；
（2）若函数y=f（x）的定义域为（-1，1），求满足不等式f（m2-1）+f（m-1）＜0的实数m的取值集合；
（3）当a∈（-∞，2）时，f（x）-4的值恒为负，求a的取值范围．
已知直线l：x-y+3=0及圆C：x2+（y-2）2=4，令圆C在x轴同侧移动且与x轴相切．
（1）圆心在何处时，圆被直线l截得的弦最长？
（2）圆心在何处时，l与y轴的交点把弦分成1：2？
已知f（x）=ax2+bx+c（a≠0）且方程f（x）=x无实数根，下列命题：
①方程f[f（x）]=x也一定没有实数根；
②若a＞0；则不等式f[f（x）]＞x对一切x都成立；
③若a＜0则必存在实数x0，使f[f（x0）]＞x0；
④若a+b+c=0则不等式f[f（x）]＜x对一切x都成立．
其中正确命题的序号是
 
．（把你认为正确命题的所有序号都填上）
已知直线l：y=-
1
2
x+1，试求：
（1）点P（-2，-1）关于直线l的对称点坐标；
（2）直线l1：y=x-2关于直线l对称的直线l2的方程；
（3）直线l关于点A（1，1）对称的直线方程．
动点P到x轴，y轴的距离之比等于非零常数k，则动点P的轨迹方程是（　　）
A、y=
x
k
（x≠0）
B、y=kx（x≠0）
C、y=-
x
k
（x≠0）
D、y=±kx（x≠0）
已知数列{an}满足：a1=1，n为正整数，对任意的n≥2都有an+2anan-1-an-1=0成立．
（1）求证：数列{
1
an
}为等差数列；并求{an}的通项公式；
（2）判断a3•a6是否为数列{an}中的项，如果是，是第几项？如果不是，说明理由；
（3）设cn=an•an+1（n∈N*），求数列{cn}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网