题目内容
15.设非零向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,若存在m∈R,使得向量4$\overrightarrow{a}$-m$\overrightarrow{b}$与$\overrightarrow{a}$-m$\overrightarrow{b}$的夹角也为θ,则cosθ的最小值是-1.分析 由题意可得,当θ=π时,满足题目条件,由此可得cosθ的最小值是-1.
解答 解:如图,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OD}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=4$\overrightarrow{a}$,$\overrightarrow{OB}$=-m$\overrightarrow{b}$,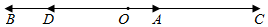
且|4$\overrightarrow{a}$|>|-m$\overrightarrow{b}$|,|$\overrightarrow{a}$|<|-m$\overrightarrow{b}$|,
则有非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为π,向量4$\overrightarrow{a}$-m$\overrightarrow{b}$与$\overrightarrow{a}$-m$\overrightarrow{b}$的夹角也为π,
此时cosθ的最小值是cosπ=-1.
故答案为:-1.
点评 本题考查数量积表示两个向量的夹角,考查了数形结合的解题思想方法,考查了想象能力和理解能力,有一定难度.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
5.线段AD、BE分别时边长为2的等边三角形ABC在边BC、AC边上的高,则$\overrightarrow{AD}$•$\overrightarrow{BE}$=( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
10.若函数f(x)同时满足以下三个性质;①f(x)的最小正周期为π;②对任意的x∈R,都有f(x-$\frac{π}{4}$)=f(-x);③f(x)在($\frac{3π}{8}$,$\frac{π}{2}$)上是减函数.则f(x)的解析式可能是( )
| A. | f(x)=cos(x+$\frac{π}{8}$) | B. | f(x)=sin2x-cos2x | C. | f(x)=sinxcosx | D. | f(x)=sin2x+cos2x |
7.在△ABC中,角A,B,C所对的边分别为a,b,c,若acosA=bsinA,且B>$\frac{π}{2}$,则sinA+sinC的最大值是( )
| A. | $\sqrt{2}$ | B. | $\frac{9}{8}$ | C. | 1 | D. | $\frac{7}{8}$ |
4.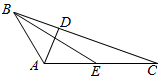 如图所示,在三角形ABC中,AD⊥BC,AD=1,BC=4,点E为AC的中点,$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$,则AB的长度为( )
如图所示,在三角形ABC中,AD⊥BC,AD=1,BC=4,点E为AC的中点,$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$,则AB的长度为( )
 如图所示,在三角形ABC中,AD⊥BC,AD=1,BC=4,点E为AC的中点,$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$,则AB的长度为( )
如图所示,在三角形ABC中,AD⊥BC,AD=1,BC=4,点E为AC的中点,$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$,则AB的长度为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |