题目内容

已知-7，a1，a2，-1四个实数成等差数列，-4，b1，b2，b3，-1五个实数成等比数列，则
a2-a1
b2
=（　　）
A、1B、-1C、2D、±1
考点：等差数列的通项公式,等比数列的通项公式
专题：等差数列与等比数列
分析：由等差数列的通项公式求得a2-a1，由等比数列的性质求得b2，作比后答案可求．
解答： 解：∵-7，a1，a2，-1四个实数成等差数列，
∴-1=-7+3d，则d=2，
∴a2-a1=2．
又-4，b1，b2，b3，-1成等比数列，
∴b22=-4×(-1)=4，则b2=-2．
∴
a2-a1
b2
=
2
-2
=-1．
故选：B．
点评：本题考查了等差数列和等比数列的通项公式，考查了等比数列的性质，是基础的计算题．
练习册系列答案
相关题目
已知球的直径PQ=4，A、B、C是该球球面上的三点，∠APQ=∠BPQ=∠CPQ=30°，△ABC是正三角形，则棱锥P-ABC的体积为
 
．
关于函数f（x）=cos2x-2
3
sinxcosx，下列命题：
①若存在x1，x2有x1-x2=π时，f（x1）=f（x2）成立；
②f（x）在区间[-
π
6
，
π
3
]上是单调递增；
③函数f（x）的图象关于点（
π
12
，0）成中心对称图象；
④将函数f（x）的图象向右平移
5π
12
个单位后将与y=2sin2x的图象重合．
其中正确的命题序号
 
（注：把你认为正确的序号都填上）
若f（x）=f（2-x），且当x∈（-∞，1）时，（x-1）f′（x）＜0，设a=f（0），b=f（
1
2
），C=f（3），则a，b，c大小关系为
 
．
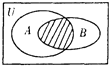
设全集U=R，A={x|x（x+2）＜0，B={x|x＜-1}，则图中阴影部分表示的集合为（　　）
A、{x|-2＜x＜0}
B、{x|-2＜x＜-1}
C、{x|x＞0}
D、{x|x＜-1}
参数方程
x=1+cosθ
y=-2+sinθ
（θ为参数）所表示的图形是（　　）
A、直线B、射线C、圆D、半圆
若α，β是两个不同平面，m，n是两条不同直线，则下列命题中不正确的是（　　）
A、α∥β，m⊥α，则m⊥β
B、m∥n，m⊥α，则n⊥α
C、n∥α，n⊥β，则α⊥β
D、α∩β=m，n与α，β所成的角相等，则m⊥n
如图，网格纸上的正方形的边长为1，粗线画出的是某几何体的三视图，则这个几何体的体积为（　　）
A、30B、50C、75D、150
函数y=3sin2x是（　　）
A、周期为2π的奇函数
B、周期为2π的偶函数
C、周期为π的奇函数
D、周期为π的偶函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网