题目内容
已知函数f(x)及其导数f′(x),若存在x0,使得f′(x0)=f(x0),则称x0是f(x)的一个“和谐点”,下列函数中①f(x)=x2;②f(x)=
;③f(x)=lnx;④f(x)=x+
,存在“和谐点”的是( )
| 1 |
| ex |
| 1 |
| x |
| A、①② | B、①④ |
| C、①③④ | D、②③④ |
考点:导数的运算
专题:导数的概念及应用
分析:分别求函数的导数,根据条件f(x0)=f′(x0),确实是否有解即可.
解答:
解:①中的函数f(x)=x2,f'(x)=2x.要使f(x)=f′(x),则x2=2x,解得x=0或2,可见函数有和谐点;
对于②中的函数,要使f(x)=f′(x),则e-x=-e-x,由对任意的x,有e-x>0,可知方程无解,原函数没有和谐点;
对于③中的函数,要使f(x)=f′(x),则lnx=
,由函数f(x)=lnx与y=
的图象它们有交点,因此方程有解,原函数有和谐点;
对于④中的函数,要使f(x)=f′(x),则x+
=1-
,即x3-x2+x+1=0,
设函数g(x)=x3-x2+x+1,g'(x)=3x2-2x+1>0且g(-1)<0,g(0)>0,
显然函数g(x)在(-1,0)上有零点,原函数有和谐点.
故答案为:①③④
故选:C
对于②中的函数,要使f(x)=f′(x),则e-x=-e-x,由对任意的x,有e-x>0,可知方程无解,原函数没有和谐点;
对于③中的函数,要使f(x)=f′(x),则lnx=
| 1 |
| x |
| 1 |
| x |
对于④中的函数,要使f(x)=f′(x),则x+
| 1 |
| x |
| 1 |
| x2 |
设函数g(x)=x3-x2+x+1,g'(x)=3x2-2x+1>0且g(-1)<0,g(0)>0,
显然函数g(x)在(-1,0)上有零点,原函数有和谐点.
故答案为:①③④
故选:C
点评:本题主要考查导数的应用,以及函数的方程的判断,对于新定义问题,关键是理解其含义,本题的本质是方程有无实根问题.

练习册系列答案
相关题目
函数f(x)图象的一部分如图所示,则f(x)的解析式可为( )


A、f(x)=4sin
| ||
B、f(x)=3.5sin
| ||
C、f(x)=3.5sin
| ||
D、f(x)=4sin
|
已知{an}是等差数列,Sn为其前n项和,若S4026-S1=0,O为坐标原点,点M(1,-a1)、N(2014,a2014),则
•
=( )
| OM |
| ON |
| A、0 | B、-1 |
| C、2014 | D、-2014 |
已知函数f(x)=
,则f(f(2))=( )
|
A、
| ||
B、
| ||
| C、2 | ||
| D、-2 |
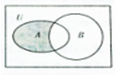
设全集U=R,A={x||x-1|<1},B={x|y=
},则图中阴影部分表示的集合是( )
| 1 | ||
|

| A、{x|x≥1} |
| B、{x|1≤x<2} |
| C、{x|0<x≤1} |
| D、{x|1≤1} |