题目内容
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小
的距离小![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,
,![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() .设线段
.设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)由题意可知:动点![]() 到定点
到定点![]() 的距离等于
的距离等于![]() 到定直线
到定直线![]() 的距离,由此利用抛物线的定义能求出点
的距离,由此利用抛物线的定义能求出点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)设![]() 两点坐标分别为
两点坐标分别为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .由题意可设直线
.由题意可设直线![]() 的方程为
的方程为![]() ,
,![]() ,由
,由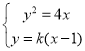 ,得
,得![]() .由此利用根的判别式、韦达定理、直线的斜率、直线方程,结合已知条件能证明直线
.由此利用根的判别式、韦达定理、直线的斜率、直线方程,结合已知条件能证明直线![]() 恒过定点
恒过定点![]() .
.
(3)求出![]() ,利用基本不等式能求出三角形面积的最小值.
,利用基本不等式能求出三角形面积的最小值.
解:(1)由题意可知:动点![]() 到定点
到定点![]() 的距离等于
的距离等于![]() 到定直线
到定直线![]() 的距离.根据抛物线的定义可知,点
的距离.根据抛物线的定义可知,点![]() 的轨迹
的轨迹![]() 是抛物线.
是抛物线.
![]() ,
,![]() 抛物线方程为:
抛物线方程为:![]()
(2)设![]() ,
,![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
由题意可设直线![]() 的方程为
的方程为![]()
![]() .
.
由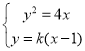 ,得
,得![]() .
.
![]() .
.
因为直线![]() 与曲线
与曲线![]() 于
于![]() ,
,![]() 两点,所以
两点,所以![]() ,
,![]() .
.
所以点![]() 的坐标为
的坐标为![]() .由题知,直线
.由题知,直线![]() 的斜率为
的斜率为![]() ,同理可得点
,同理可得点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,有
时,有![]() ,此时直线
,此时直线![]() 的斜率
的斜率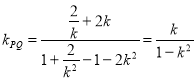 .
.
所以,直线![]() 的方程为
的方程为![]() ,整理得
,整理得![]() .
.
于是,直线![]() 恒过定点
恒过定点![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,也过点
,也过点![]() .
.
综上所述,直线![]() 恒过定点
恒过定点![]() .
.
(3)可求得![]() .所以
.所以![]() 面积
面积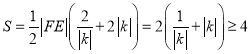 .
.
当且仅当![]() 时,“
时,“![]() ”成立,所以
”成立,所以![]() 面积的最小值为
面积的最小值为![]() .
.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目