题目内容
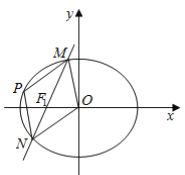
【题目】已知抛物线![]() ,的焦点为
,的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,
,![]() 两点,抛物线在点
两点,抛物线在点![]() ,
,![]() 处的切线分别为
处的切线分别为![]() ,
,![]() ,两条切线的交点为
,两条切线的交点为![]() .
.
(1)证明:![]() ;
;
(2)若![]() 的外接圆
的外接圆![]() 与抛物线
与抛物线![]() 有四个不同的交点,求直线
有四个不同的交点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)证明见解析(2)![]() 或
或![]()
【解析】
(1)联立直线![]() 与抛物线的方程,利用根于系数关系,结合斜率表达式求得
与抛物线的方程,利用根于系数关系,结合斜率表达式求得![]() 即可;
即可;
(2)由(1)可知,圆![]() 是以
是以![]() 为直径的圆且圆
为直径的圆且圆![]() 的方程可化简为
的方程可化简为![]() ,联立圆与抛物线的方程得到
,联立圆与抛物线的方程得到![]() ,圆
,圆![]() 与抛物线
与抛物线![]() 有四个不同的交点等价于
有四个不同的交点等价于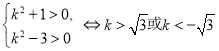
解:(1)证明:依题意有![]() ,直线
,直线![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交,
相交,
联立方程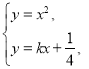 消去
消去![]() ,化简得
,化简得![]() ,
,
所以,![]() .
.
又因为![]() ,所以直线
,所以直线![]() 的斜率
的斜率![]() .
.
同理,直线![]() 的斜率
的斜率![]() ,
,
所以,![]() ,
,
所以,直线![]() ,即
,即![]() .
.
(2)由(1)可知,圆![]() 是以
是以![]() 为直径的圆,
为直径的圆,
设![]() 是圆
是圆![]() 上的一点,则
上的一点,则![]() ,
,
所以,圆![]() 的方程为
的方程为![]() ,
,
又因为![]() ,
,
所以,圆![]() 的方程可化简为
的方程可化简为![]() ,
,
联立圆![]() 与抛物线
与抛物线![]() 得
得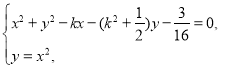
消去![]() ,得
,得![]() ,
,
即![]() ,即
,即![]() ,
,
若方程![]() 与方程
与方程![]() 有相同的实数根
有相同的实数根![]() ,
,
则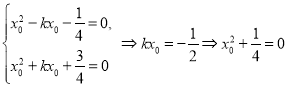 ,矛盾,
,矛盾,
所以,方程![]() 与方程
与方程![]() 没有相同的实数根,
没有相同的实数根,
所以,圆![]() 与抛物线
与抛物线![]() 有四个不同的交点等价于
有四个不同的交点等价于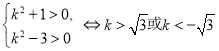 ,
,
综上所述,![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案【题目】垃圾种类可分为可回收垃圾、干垃圾、湿垃圾、有害垃圾等,为调查中学生对垃圾分类的了解程度,某调查小组随机从本市一中高一的![]() 名学生(其中女生
名学生(其中女生![]() 人)中,采用分层抽样的方法抽取
人)中,采用分层抽样的方法抽取![]() 名学生进行调查,已知抽取的
名学生进行调查,已知抽取的![]() 名学生中有男生
名学生中有男生![]() 人、
人、
(1)求![]() 值及抽到的女生人数;
值及抽到的女生人数;
(2)调查小组请这![]() 名学生指出生活中若干项常见垃圾的种类,把能准确分类不少于
名学生指出生活中若干项常见垃圾的种类,把能准确分类不少于![]() 项的称为“比较了解”,少于三项的称为“不太了解”,调查结果如下:
项的称为“比较了解”,少于三项的称为“不太了解”,调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
男生(人) | 4 | 22 | 34 | 18 | 16 | 10 | 6 |
女生(人) | 0 | 15 | 20+m | 20 | 16 | 9 | m |
求![]() 值,完成如下
值,完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为学生对垃圾分类的了解程度与性别有关?
的把握认为学生对垃圾分类的了解程度与性别有关?
不太了解 | 比较了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
(3)在(2)条件下,从抽取的“比较了解”的学生中仍采用分层抽样的方法抽取![]() 名.再从这
名.再从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人作义务讲解员,求抽取的
人作义务讲解员,求抽取的![]() 人中至少一名女生的概率.
人中至少一名女生的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
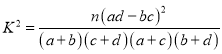 ,
,![]()