题目内容

9．已知曲线f（x）=$\frac{{a{x^2}}}{x+1}$在点（1，f（1））处切线的斜率为1，则实数a的值为（　　）
A．$\frac{3}{2}$B．$-\frac{3}{2}$C．$-\frac{3}{4}$D．$\frac{4}{3}$

分析 首先求出函数的导数，然后求出f'（1）=1，进而求出a的值．

解答 解：∵f'（x）=$\frac{a{x}^{2}+2ax}{（x+1）^{2}}$，曲线f（x）=$\frac{{a{x^2}}}{x+1}$在点（1，f（1））处切线的斜率为1，
∴f'（1）=$\frac{3a}{4}$=1
解得：a=$\frac{4}{3}$．
故选：D．

点评 本题考查了导数的运算以及导数与斜率的关系，比较容易，属于基础题．

练习册系列答案
相关题目
19．△ABC的三边长分别为|AB|=7，|BC|=5，|CA|=6，则$\overrightarrow{AB}$•$\overrightarrow{BC}$ 的值为（　　）
A．19B．14C．-18D．-19
20．已知命题p：?x∈（-∞，0），2x＜3x；命题q：?x∈（0，$\frac{π}{2}$），sinx＜x，则下列命题为真命题的是（　　）
A．p∧qB．p∨（￢q）C．（￢p）∧qD．p∧（￢q）
17．已知公差不为0的等差数列{an}满足a1，a3，a4成等比数列，Sn为数列{an}的前n项和，则$\frac{{{S_4}-{S_2}}}{{{S_5}-{S_3}}}$的值为（　　）
A．-2B．-3C．2D．3
4．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）单调递增．若实数a满足f（log2a）+f（log${\;}_{\frac{1}{2}}$a）＜2f（1），则a的取值范围（　　）
A．[1，2]B．（0，$\frac{1}{2}$]C．（$\frac{1}{2}$，2）D．（0，2]
14．已知数列{an}的前n项和为Sn，a1=1，an+1=3Sn+2，则a4=（　　）
A．64B．80C．256D．320
1．已知函数f（x）=2sinxcosx-$\sqrt{3}cos2x（{x∈R}）$．
（1）若f（a）=$\frac{1}{2}$且$a∈（{\frac{5π}{12}，\frac{2π}{3}}）$，求cos2a；
（2）求曲线y=f（x）在点（0，f（0））处的切线方程；
（3）记函数f（x）在$x∈[{\frac{π}{4}，\frac{π}{2}}]$上的最大值为b，且函数f（x）在[aπ，bπ]（a＜b）上单调递增，求实数a的最小值．
18．若$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（-1，1），（2$\overrightarrow{a}$+$\overrightarrow{b}$）∥（$\overrightarrow{a}$-m$\overrightarrow{b}$），则m=（　　）
A．$\frac{1}{2}$B．2C．-2D．-$\frac{1}{2}$
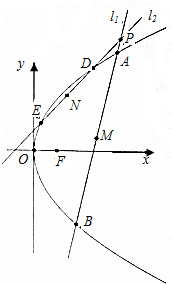10．已知抛物线C：y2=2px（p＞0）的焦点为F，定点P（3，4）到焦点F的距离为2$\sqrt{5}$且线段PF与抛物线C有公共点，过点P的动直线l1，l2的斜率分别为k1，k2，且满足k1+k2=4，若l1交抛物线C于A，B两点，l2交抛物线C于D，E两点，弦AB，DE的中点分别为M，N．
（1）求抛物线C的方程；
（2）求证：直线MN过定点Q，并求出定点Q的坐标；
（3）若4$\overrightarrow{QM}$=$\overrightarrow{QN}$，求出直线MN的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网