Question

9．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1（x≤1）}\\{2x-3（x＞1）}\\{\;}\end{array}\right.$
（1）做出函数的图象；
（2）求f[f（-2）]；
（3）若f（a）=5，求a的值．

Answer 1

分析 （1）分段作出函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1（x≤1）}\\{2x-3（x＞1）}\\{\;}\end{array}\right.$ 的图象即可，
（2）先求f（-2）=（-2）²+1=5，从而可求得f[f（-2）]=f（5）=10-3=7；
（3）由（2）知a=-2是方程f（a）=5的解，再求a＞1时的即可．

解答 解：（1）作函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1（x≤1）}\\{2x-3（x＞1）}\\{\;}\end{array}\right.$ 的图象如下，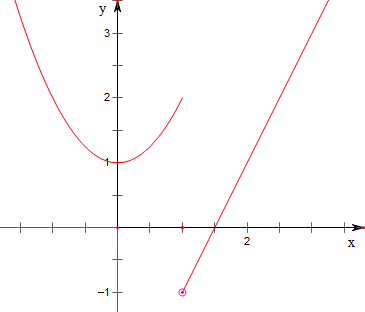

（2）f（-2）=（-2）²+1=5，
f[f（-2）]=f（5）=10-3=7；
（3）由（2）知，当a≤1时，a=-2是方程f（a）=5的解，
当a＞1时，f（a）=2a-3=5，解得，a=4；
故a=-2或a=4．

点评 本题考查了分段函数的应用及数形结合的思想应用．