题目内容
7.已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$E({\sqrt{3},\frac{1}{2}})$,且离心率为$\frac{{\sqrt{3}}}{2}$.(1)求椭圆Γ的方程;
(2)直线l与圆O:x2+y2=b2相切于点M,且与椭圆Γ相交于不同的两点A,B,求|AB|的最大值.
分析 (1)将E代入椭圆方程,根据椭圆的离心率公式,即可求得a和b的值,求得椭圆方程;
(2)分类讨论,当直线l不垂直于x轴时,设直线l的方程为y=kx+m,代入椭圆方程,由韦达定理及弦长公式求得丨AB丨,根据基本不等式的性质即可求得丨AB丨的最大值.
解答 解:(1)将$E({\sqrt{3},\frac{1}{2}})$代入椭圆方程,$\frac{3}{a^2}+\frac{1}{{4{b^2}}}=1$,
由椭圆的离心率e=$\frac{c}{a}$=$\frac{{\sqrt{{a^2}-{b^2}}}}{a}=\frac{{\sqrt{3}}}{2}$,
解得:a=2,b=1,
∴椭圆Γ的方程为$\frac{x^2}{4}+{y^2}=1$.
(2)当直线l垂直于x轴时,由直线l与圆O:x2+y2=1相切,
可知直线l的方程为x=±1,易求$|{AB}|=\sqrt{3}$.
当直线l不垂直于x轴时,设直线l的方程为y=kx+m,
由直线l与圆O:x2+y2=1相切,得$\frac{|m|}{{\sqrt{{k^2}+1}}}=1$,即m2=k2+1,
将y=kx+m代入$\frac{x^2}{4}+{y^2}=1$,整理得(1+4k2)x2+8kmx+4m2-4=0,
设A(x1,y1),B(x2,y2),则${x_1}+{x_2}=\frac{-8km}{{1+4{k^2}}}$,${x_1}{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}$,
$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\sqrt{1+{k^2}}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}$=$\sqrt{1+{k^2}}\sqrt{{{({\frac{-8km}{{1+4{k^2}}}})}^2}-\frac{{16{m^2}-16}}{{1+4{k^2}}}}=4\sqrt{1+{k^2}}\frac{{\sqrt{1+4{k^2}-{m^2}}}}{{1+4{k^2}}}$,
又因为m2=k2+1,
所以$|{AB}|=\frac{{4\sqrt{3}|k|\sqrt{{k^2}+1}}}{{1+4{k^2}}}≤\frac{{2({3{k^2}+{k^2}+1})}}{{1+4{k^2}}}=2$,
当且仅当$\sqrt{3}|k|=\sqrt{{k^2}+1}$,即$k=±\frac{{\sqrt{2}}}{2}$时等号成立,
综上所述,|AB|的最大值为2.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,弦长公式,考查分类讨论思想,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $(-∞,\frac{9}{4}]$ | B. | $[\frac{7}{4},+∞)$ | C. | $[\frac{7}{4},\frac{9}{4}]$ | D. | $(-∞,\frac{7}{4}]∪$$[\frac{9}{4},+∞)$ |
| A. | $-\frac{1}{5}-\frac{3}{5}i$ | B. | $\frac{1}{5}+\frac{3}{5}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $\frac{1}{5}-\frac{3}{5}i$ |
| A. | 4 | B. | -1 | C. | -2 | D. | -3 |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
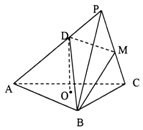 如图,三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
如图,三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.