题目内容
10.已知数列{bn}为等差数列,数列{an}为递增等比数列,${a}_{5}^{2}$=a10,且2(an+an+2)=5an+1,n∈N*,且b1=a3,b3=a4.(1)求数列{an}和{bn}的通项公式;
(2)令cn=an•bn,求数列{cn}的前n项和Sn.
分析 (1)利用递增等比数列的通项公式及性质,求出首项和公差,由此能求出数列{an}的通项公式;从而求出b1=a3=8,b3=a4=16,利用等差数列性质求出公差,由此能求出{bn}的通项公式.
(2)由cn=an•bn=(4n+4)•2n=(n+1)•2n+2,利用错位相减法能求出数列{cn}的前n项和.
解答 解:(1)∵数列{an}为递增等比数列,${a}_{5}^{2}$=a10,且2(an+an+2)=5an+1,n∈N*,
∴(a1q4)2=a1q9,2(1+q2)=5q,
∵等比数列{an}为递增数列,
∴q=2,a1=2
∴an=2n.
∵数列{bn}为等差数列,b1=a3=8,b3=a4=16,
∴b3=8+2d=16,解得d=4,
∴bn=8+(n-1)×4=4n+4.
(2)∵cn=an•bn=(4n+4)•2n=(n+1)•2n+2,
∴数列{cn}的前n项和:
Sn=2•23+3•24+4•25+…+(n+1)•2n+2,①
$2{S}_{n}=2•{2}^{4}+3•{2}^{5}+4•{2}^{6}+…+(n+1)•{2}^{n+3}$,②
①-②,得:-Sn=16+24+25+26+…+2n+2-(n+1)•2n+3
=16+$\frac{16(1-{2}^{n-1})}{1-2}$-(n+1)•2n+3
=-n•2n+3.
∴Sn=n•2n+3.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
18.已知数列{an}的前n项和Sn=$\frac{1}{2}$n(n+1),n∈N*,bn=3n+(-1)n-1an,则数列{bn}的前2n+1项和为( )
| A. | $\frac{{3}^{2n+2}-1}{2}$+n | B. | $\frac{1}{2}$•32n+2+n+$\frac{1}{2}$ | C. | $\frac{{3}^{2n+2}-1}{2}$-n | D. | $\frac{1}{2}$•32n+2-n+$\frac{3}{2}$ |
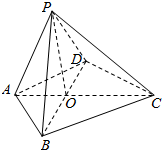 如图,四棱锥P-ABCD中,BC=CD,AB=AD=$\sqrt{2}$,AB⊥AD,O为BD的中点,PO⊥平面ABCD,平面PAB⊥平面PBC,设OC=a,PO=b.
如图,四棱锥P-ABCD中,BC=CD,AB=AD=$\sqrt{2}$,AB⊥AD,O为BD的中点,PO⊥平面ABCD,平面PAB⊥平面PBC,设OC=a,PO=b.