题目内容
9.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,其左、右焦点分别为F1,F2,点P(x0,y0)是坐标平面内一点,且x02+y02=$\frac{7}{4}$.(1)求椭圆C的方程;
(2)过点S(0,-$\frac{1}{3}$)且斜率为k的动直线l交椭圆于A、B两点,问:在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标和△MAB面积的最大值;若不存在,说明理由.
分析 (1)设F1(-c,0),F2(c,0),运用向量的数量积的坐标表示,结合条件,可得c=1,再由离心率公式,可得a,由a,b,c的关系可得b,进而得到椭圆方程;
(2)设动直线l的方程为y=kx-$\frac{1}{3}$,代入椭圆方程,运用韦达定理,假设在y轴上存在定点M(0,m),满足题设,求得向量MA,MB的坐标,再由数量积为0,化简整理,可得m=1,在y轴上存在定点M,使得以AB为直径的圆恒过这个点;求得M到AB的距离,弦长AB,由△MAB的面积公式,化简整理,再设1+2k2=t(t≥1),转化为t的式子,配方即可得到所求最大值.
解答 解:(1)设F1(-c,0),F2(c,0),
由$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=$\frac{3}{4}$,即为(-c-x0,-y0)•(c-x0,-y0)=$\frac{3}{4}$,
即有x02+y02-c2=$\frac{3}{4}$,又x02+y02=$\frac{7}{4}$,
解得c=1,又e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,则a=$\sqrt{2}$,b=1,
因此所求椭圆的方程为:$\frac{{x}^{2}}{2}$+y2=1;
(2)动直线l的方程为y=kx-$\frac{1}{3}$,
由$\left\{\begin{array}{l}{y=kx-\frac{1}{3}}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,得(1+2k2)x2-$\frac{4}{3}$kx-$\frac{16}{9}$=0,
设A(x1,y1),B(x2,y2),
则x1+x2=$\frac{4k}{3(1+2{k}^{2})}$,x1x2=-$\frac{16}{9(1+2{k}^{2})}$,
假设在y轴上存在定点M(0,m),满足题设,则
$\overrightarrow{MA}$=(x1,y1-m),$\overrightarrow{MB}$=(x2,y2-m),
$\overrightarrow{MA}$•$\overrightarrow{MB}$=x1x2+(y1-m)(y2-m)=x1x2+y1y2-m(y1+y2)+m2
=x1x2+(kx1-$\frac{1}{3}$)(kx2-$\frac{1}{3}$)-m(kx1-$\frac{1}{3}$+kx2-$\frac{1}{3}$)+m2
=(1+k2)x1x2-k($\frac{1}{3}$+m)(x1+x2)+m2+$\frac{2}{3}$m+$\frac{1}{9}$
=-$\frac{16(1+{k}^{2})}{9(1+2{k}^{2})}$-k($\frac{1}{3}$+m)•$\frac{4k}{3(1+2{k}^{2})}$+m2+$\frac{2}{3}$m+$\frac{1}{9}$
=$\frac{18({m}^{2}-1){k}^{2}+(9{m}^{2}+6m-15)}{9(2{k}^{2}+1)}$,
由假设得对于任意的k∈R,$\overrightarrow{MA}$•$\overrightarrow{MB}$=0恒成立,
即$\left\{\begin{array}{l}{{m}^{2}-1=0}\\{9{m}^{2}+m-15=0}\end{array}\right.$,解得m=1.
因此,在y轴上存在定点M,使得以AB为直径的圆恒过这个点,
点M的坐标为(0,1)这时,点M到AB的距离d=$\frac{4}{3\sqrt{1+{k}^{2}}}$,
|AB|=$\sqrt{(1+{k}^{2})({x}_{1}-{x}_{2})^{2}}$,
S△MAB=$\frac{1}{2}$|AB|d=$\frac{2}{3}$$\sqrt{({x}_{1}-{x}_{2})^{2}}$=$\frac{2}{3}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\frac{2}{3}$$\sqrt{\frac{16{k}^{2}}{2(1+2{k}^{2})^{2}}+\frac{64}{9(1+2{k}^{2})}}$=$\frac{8}{9}$$\sqrt{\frac{4+9{k}^{2}}{(1+2{k}^{2})^{2}}}$,
设1+2k2=t则k2=$\frac{t-1}{2}$得t∈[1,+∞),$\frac{1}{t}$∈(0,1],
所以$\frac{8}{9}$$\sqrt{\frac{9}{2t}-\frac{1}{2{t}^{2}}}$=$\frac{8}{9}$$\sqrt{\frac{1}{2}[\frac{81}{4}-(\frac{1}{t}-\frac{9}{2})^{2}]}$≤$\frac{16}{9}$,
当且仅当$\frac{1}{t}$=1时,上式等号成立.因此,△MAB面积的最大值是$\frac{16}{9}$.
点评 通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案| A. | $\frac{100π}{3}$cm3 | B. | $\frac{208π}{3}$cm3 | C. | $\frac{500π}{3}$cm3 | D. | $\frac{416\sqrt{3}π}{3}$cm3 |
①若x2+y2=0,则x=y=0
②“若a,b都是偶数,则a+b是偶数”的逆否命题
③“若x=2,则x2-3x+2=0”的逆命题
④“若两个三角形全等,则这两个三角形的面积相等”的否命题
其中真命题的序号是( )
| A. | ① | B. | ①②③④ | C. | ①②③ | D. | ①② |
| A. | $\frac{{3}^{2n+2}-1}{2}$+n | B. | $\frac{1}{2}$•32n+2+n+$\frac{1}{2}$ | C. | $\frac{{3}^{2n+2}-1}{2}$-n | D. | $\frac{1}{2}$•32n+2-n+$\frac{3}{2}$ |
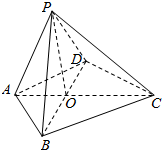 如图,四棱锥P-ABCD中,BC=CD,AB=AD=$\sqrt{2}$,AB⊥AD,O为BD的中点,PO⊥平面ABCD,平面PAB⊥平面PBC,设OC=a,PO=b.
如图,四棱锥P-ABCD中,BC=CD,AB=AD=$\sqrt{2}$,AB⊥AD,O为BD的中点,PO⊥平面ABCD,平面PAB⊥平面PBC,设OC=a,PO=b.