题目内容
8．设集合P={x|-x-6＜0}，Q={x|x-a≥0}，若P⊆Q，则实数a的取值范围是a≤-6．分析 由已知中，集合P={x|-x-6＜0}，解二次不等式求出集合P，再由Q={x|x-a≥0}，若P⊆Q，我们可以构造一个关于a的不等式，解不等式，即可得到实数a的取值范围．
解答 解：由集合P={x|-x-6＜0}得到P={x|-x-6＜0}=（-6，+∞），
∵Q={x|x-a≥0}=[a，+∞），若P⊆Q，
∴a≤-6．
故答案是：a≤-6．
点评 本题考查的知识点是集合关系中的参数取值问题，其中根据集合包含关系，构造出关于参数a的不等式是解答本题的关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
13．为了得到函数=4sin（2x+$\frac{π}{5}$），x∈R的图象，只需把函数y=4sin（x+$\frac{π}{5}$），x∈R的图象上所有点的（ ）
| A． | 横坐标伸长到原来的2倍，纵坐标不变 | |
| B． | 纵坐标伸长到原来的2倍，横坐标不变 | |
| C． | 横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变 | |
| D． | 纵坐标缩短到原来的$\frac{1}{2}$倍，横坐标不变 |
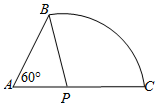某柱体实心铜制零件的截面边长是长度为55毫米线段AB和88毫米的线段AC以及圆心为P，半径为PB的一段圆弧BC构成，其中∠BAC=60°．
如图，在圆锥PO中，已知PO=$\sqrt{2}$，⊙O 的直径AB=2，C是弧$\widehat{AB}$的中点，D为AC的中点．