Question

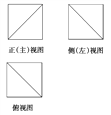
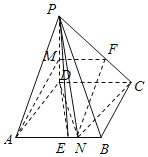
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，PD⊥平面ABCD，PD=AD=3，PM=2MD，AN=2NB，∠DAB=60°．

（1）求证：直线AM∥平面PNC；

（2）求二面角D﹣PC﹣N的余弦值．

Answer 1

【答案】（1）见解析；（2）.

【解析】试题分析：（1）在上取一点，使，连接， ，可得， ， 为平行四边形，即，即可得直线平面．

（2）取中点，可得， ， 相互垂直，以为原点，如图建立空间直角坐标系，易知平面的法向量，求出面的法向量，计算出两向量夹角即可.

试题解析：（1）在上取一点，使，连接， ，

∵， ，∴， ， ， ∴， ，∴为平行四边形，即，又平面，∴直线平面．

（2）取中点，底面是菱形， ，∴，∵，∴，即，又平面，∴，又，∴直线平面，故， ， 相互垂直，以为原点，如图建立空间直角坐标系．

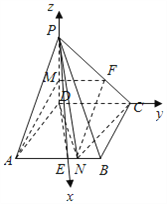
则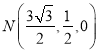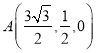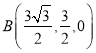， ， ， ， ， ，易知平面的法向量，设面的法向量，由，得，∴，故二面角的余弦值为