题目内容
(2013•湖北)设x,y,z∈R,且满足: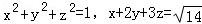 ,则x+y+z= _________ .
,则x+y+z= _________ .
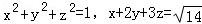 ,则x+y+z= _________ .
,则x+y+z= _________ .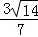
根据柯西不等式,得
(x+2y+3z)2≤(12+22+32)(x2+y2+z2)=14(x2+y2+z2)
当且仅当 时,上式的等号成立
时,上式的等号成立
∵x2+y2+z2=1,∴(x+2y+3z)2≤14,
结合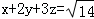 ,可得x+2y+3z恰好取到最大值
,可得x+2y+3z恰好取到最大值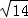
∴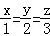 =
=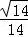 ,可得x=
,可得x=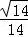 ,y=
,y=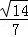 ,z=
,z=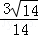
因此,x+y+z=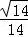 +
+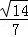 +
+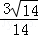 =
=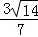
故答案为: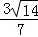
(x+2y+3z)2≤(12+22+32)(x2+y2+z2)=14(x2+y2+z2)
当且仅当
 时,上式的等号成立
时,上式的等号成立∵x2+y2+z2=1,∴(x+2y+3z)2≤14,
结合
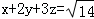 ,可得x+2y+3z恰好取到最大值
,可得x+2y+3z恰好取到最大值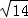
∴
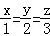 =
=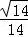 ,可得x=
,可得x=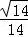 ,y=
,y=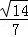 ,z=
,z=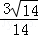
因此,x+y+z=
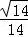 +
+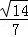 +
+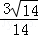 =
=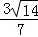
故答案为:
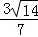

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
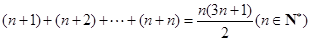
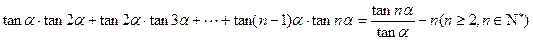
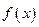 是定义域为正整数集的函数,对于定义域内任意的
是定义域为正整数集的函数,对于定义域内任意的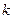 ,若
,若 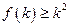 成立,则
成立,则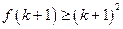 成立,下列命题成立的是
成立,下列命题成立的是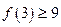 成立,则对于任意
成立,则对于任意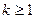 ,均有
,均有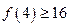 成立,则对于任意的
成立,则对于任意的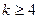 ,均有
,均有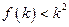 成立;
成立;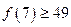 成立,则对于任意的
成立,则对于任意的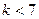 ,均有
,均有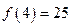 成立,则对于任意的
成立,则对于任意的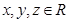 ,且
,且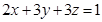 ,则
,则 的最小值是 .
的最小值是 .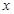 使
使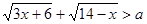 成立,求常数
成立,求常数 的取值范围 .
的取值范围 . .
. 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘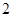 ,纵坐标乘
,纵坐标乘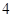 ,变到点
,变到点 .
.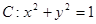 在变换
在变换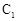 的极坐标方程为:
的极坐标方程为: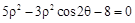 ,直线
,直线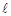 的参数方程为:
的参数方程为: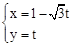 (
(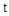 为参数).
为参数).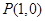 ,曲线
,曲线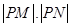 的值.
的值.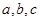 为实数,且
为实数,且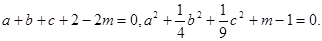
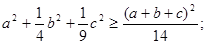
 πR2
πR2 πR2
πR2 πR2
πR2