题目内容
用数学归纳法证明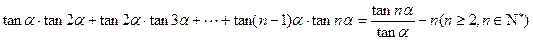
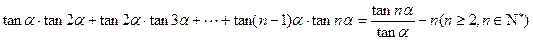
(1)当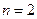 时,左边
时,左边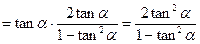
右边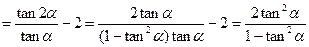 ,等式成立.
,等式成立.
(2)假设当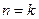 时,
时,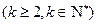 等式成立,即
等式成立,即
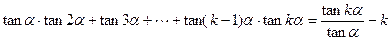
则当 时,
时,
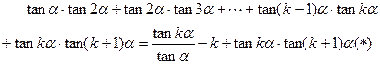
由 得
得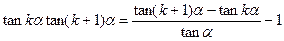
代入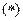 式,得
式,得
右边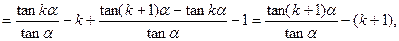
即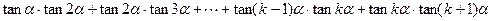
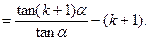
这就是说,当 时等式成立.
时等式成立.
根据(1)、(2)可知,对任意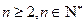 ,等式成立
,等式成立
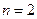 时,左边
时,左边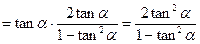
右边
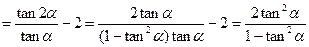 ,等式成立.
,等式成立.(2)假设当
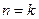 时,
时,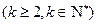 等式成立,即
等式成立,即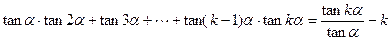
则当
 时,
时,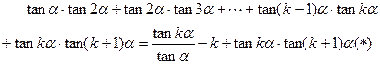
由
 得
得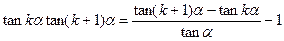
代入
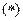 式,得
式,得右边
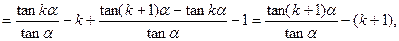
即
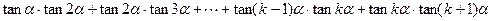
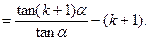
这就是说,当
 时等式成立.
时等式成立.根据(1)、(2)可知,对任意
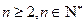 ,等式成立
,等式成立在由假设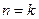 时等式成立,推导当
时等式成立,推导当 时等式成立时,要灵活应用三角公式及其变形公式,本题中涉及到两个角的正切的乘积问题,联想到两角差的正切公式的变形公式:
时等式成立时,要灵活应用三角公式及其变形公式,本题中涉及到两个角的正切的乘积问题,联想到两角差的正切公式的变形公式: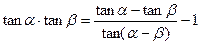 ,问题就会迎刃而解
,问题就会迎刃而解
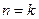 时等式成立,推导当
时等式成立,推导当 时等式成立时,要灵活应用三角公式及其变形公式,本题中涉及到两个角的正切的乘积问题,联想到两角差的正切公式的变形公式:
时等式成立时,要灵活应用三角公式及其变形公式,本题中涉及到两个角的正切的乘积问题,联想到两角差的正切公式的变形公式: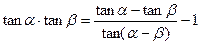 ,问题就会迎刃而解
,问题就会迎刃而解
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
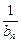 )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与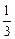 logabn+1的大小,并证明你的结论
logabn+1的大小,并证明你的结论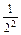 +
+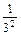 +…+
+…+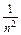 ≥
≥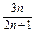 (n∈N*).
(n∈N*).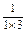 +
+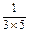 +…+
+…+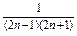 =
=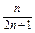 .
. 中,
中,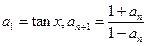 ,
,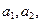
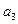 ;(2)求数列
;(2)求数列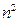 与
与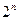 的大小
的大小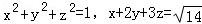 ,则x+y+z= _________ .
,则x+y+z= _________ .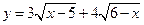 的最大值。
的最大值。