题目内容
(本小题满分12分)用数学归纳法证明: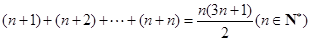
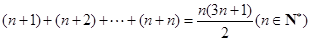
见解析
(1)当 时,左边
时,左边 ,
,
右边 左边,等式成立.
左边,等式成立.
(2)假设 时等式成立,即
时等式成立,即 .
.
则当 时,左边
时,左边



 ,
,
 时,等式也成立.
时,等式也成立.
由(1)和(2)知对任意 ,等式成立.
,等式成立.
 时,左边
时,左边 ,
,右边
 左边,等式成立.
左边,等式成立.(2)假设
 时等式成立,即
时等式成立,即 .
.则当
 时,左边
时,左边



 ,
, 时,等式也成立.
时,等式也成立.由(1)和(2)知对任意
 ,等式成立.
,等式成立.
练习册系列答案
相关题目
题目内容
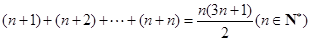
 时,左边
时,左边 ,
, 左边,等式成立.
左边,等式成立. 时等式成立,即
时等式成立,即 .
. 时,左边
时,左边



 ,
, 时,等式也成立.
时,等式也成立. ,等式成立.
,等式成立.