题目内容
7.已知${(1+x)^{10}}={a_0}+{a_1}(1-x)+{a_2}{(1-x)^2}+…+{a_{10}}{(1-x)^{10}}$,则a9等于-20.分析 由条件利用(1+x)10=(-1-x)10=[(-2)+(1-x)]10,以及二项展开式的通项公式,求得a9的值.
解答 解:∵(1+x)10=(-1-x)10=[(-2)+(1-x)]10,
${(1+x)^{10}}={a_0}+{a_1}(1-x)+{a_2}{(1-x)^2}+…+{a_{10}}{(1-x)^{10}}$,
∴a9=${C}_{10}^{9}$•(-2)=-20,
故答案为:-20.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
17.已知函数 f(x)=kx($\frac{1}{e}$≤x≤e2),与函数$g(x)={(\frac{1}{e})^{\frac{x}{2}}}$,若f(x)与g(x)的图象上分别存在点M,N,使得MN关于直线y=x对称,则实数k的取值范围是( )
| A. | [-$\frac{1}{e}$,e] | B. | [-$\frac{2}{e}$,2e] | C. | (-$\frac{2}{e}$,2e) | D. | [-$\frac{3}{e}$,3e] |
19.如图,在正六边形ABCDEF,点O为其中心,则下列判断错误的是( )
| A. | $\overrightarrow{AB}=\overrightarrow{OC}$ | B. | $\overrightarrow{AB}∥\overrightarrow{DE}$ | C. | $|{\overrightarrow{AD}}|=|{\overrightarrow{BE}}|$ | D. | $|{\overrightarrow{AC}}|=|{\overrightarrow{BE}}|$ |
16.若直线ax+by=1与圆x2+y2=1相交,则点P(a,b)与圆的位置关系是( )
| A. | 在圆上 | B. | 在圆外 | C. | 在圆内 | D. | 不能确定 |
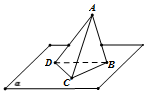 如图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=4,AD=2$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是 $2\sqrt{3}π$.
如图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=4,AD=2$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是 $2\sqrt{3}π$.