题目内容
17.已知关于x的方程(t+1)cosx-tsinx=t+2在(0,π)上有实根.则实数t的最大值是-1.分析 分离参数可得t=$\frac{2-cosx}{cosx-sinx-1}$,利用导数判断右侧函数的单调性求出最大值即可.
解答 解:∵(t+1)cosx-tsinx=t+2,
∴t=$\frac{2-cosx}{cosx-sinx-1}$,
令f(x)=$\frac{2-cosx}{cosx-sinx-1}$,
则f′(x)=$\frac{sinx(cosx-sinx-1)-(2-cosx)(-sinx-cosx)}{(cosx-sinx-1)^{2}}$=$\frac{sinx+2cosx-1}{(cosx-sinx-1)^{2}}$,
令g(x)=sinx+2cosx-1,则g′(x)=cosx-2sinx,
∴当x=arctan$\frac{1}{2}$时,g′(x)=0,当0<x<arctan$\frac{1}{2}$时,g′(x)>0,当arctan$\frac{1}{2}$<x<π时,g′(x)<0,
∴g(x)在(0,arctan$\frac{1}{2}$)上单调递增,在(arctan$\frac{1}{2}$,π)上单调递减,
又g(0)=1,g(π)=-3,
∴g(x)在(0,π)上只有一个零点,又g($\frac{π}{2}$)=0,
∴当0<x<$\frac{π}{2}$时,g(x)>0,当$\frac{π}{2}$<x<π时,g(x)<0,
∴当0<x<$\frac{π}{2}$时,f′(x)>0,当$\frac{π}{2}$<x<π时,f′(x)<0
∴f(x)在(0,$\frac{π}{2}$)上单调递增,在($\frac{π}{2}$,0)上单调递减,
∴当x=$\frac{π}{2}$时,f(x)取得最大值f($\frac{π}{2}$)=-1.
∴t的最大值为-1.
故答案为-1.
点评 本题考查了导数与函数单调性的关系,函数最值的计算,属于中档题.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
| A. | 在圆上 | B. | 在圆外 | C. | 在圆内 | D. | 以上皆有可能 |
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 与a的大小有关 |
| A. | $(\frac{1}{e},2)∪(2,e)$ | B. | $(\frac{1}{e}+1,e)$ | C. | (e-1,e) | D. | $(\frac{1}{e},e)$ |
| 零件数(个) | 18 | 20 | 22 |
| 加工时间y(分钟) | 27 | 30 | 33 |
| A. | 84分钟 | B. | 94分钟 | C. | 102分钟 | D. | 112分钟 |
| A. | (-∞,-1) | B. | (-1,0) | C. | (-2,-1) | D. | (-∞,0)∪(0,1) |
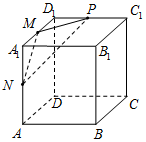 正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )
正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $12\sqrt{3}$ |