题目内容
(本小题满分14分)
已知数列 的前
的前 项和
项和 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,是否存在
,是否存在
 ,使得
,使得 、
、 、
、 成等比数列.若存在,求出所有符合条件的
成等比数列.若存在,求出所有符合条件的 值;若不存在,请说明理由.
值;若不存在,请说明理由.
(1) ;(2)不存在k.
;(2)不存在k.
【解析】
试题分析:本题主要考查由 求
求 、等比中项、均值定理、对数的性质、反证法等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力. 第一问,由
、等比中项、均值定理、对数的性质、反证法等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力. 第一问,由 计算得到
计算得到 ,从而判断出数列
,从而判断出数列 是首项为
是首项为 的常数列,即
的常数列,即 ,所以
,所以 ;第二问,用反证法,先利用等比中项列出
;第二问,用反证法,先利用等比中项列出 ,再代入
,再代入 中,利用均值定理进行变形,再利用对数的性质化简,从而得到
中,利用均值定理进行变形,再利用对数的性质化简,从而得到 ,得到矛盾,从而证出所求证的结论.
,得到矛盾,从而证出所求证的结论.
试题解析:(1)解法1:当 时,
时, , 2分
, 2分
即
 . 4分
. 4分
∴数列 是首项为
是首项为 的常数列. 5分
的常数列. 5分
∴ ,即
,即
 .
.
∴数列 的通项公式为
的通项公式为
 . 7分
. 7分
解法2:当 时,
时, , 2分
, 2分
∴
 . 4分
. 4分

 . 5分
. 5分
∵ ,符合
,符合 的表达式. 6分
的表达式. 6分
∴数列 的通项公式为
的通项公式为
 . 7分
. 7分
(2)假设存在
 ,使得
,使得 、
、 、
、 成等比数列,
成等比数列,
则
 . 8分
. 8分
∵
 ,
,
∴ 11分
11分
 . 13分
. 13分
这与
 矛盾.
矛盾.
∴不存在
 ,使得
,使得 、
、 、
、 成等比数列. 14分
成等比数列. 14分
考点:由 求
求 、等比中项、均值定理、对数的性质、反证法.
、等比中项、均值定理、对数的性质、反证法.

练习册系列答案
相关题目
 ,集合
,集合 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 是定义在
是定义在 上的奇函数,若对于任意两个实数
上的奇函数,若对于任意两个实数 ,不等式
,不等式 恒成立,则不等式
恒成立,则不等式 的解集为( )
的解集为( ) B.
B. C.
C. D.
D.
 的定义域为( )
的定义域为( ) B.
B. C.
C. D.
D.
 的参数方程为
的参数方程为 (
( 为参数),圆C的参数方程为
为参数),圆C的参数方程为 (
( 为参数).若直线
为参数).若直线 ,满足对任意的
,满足对任意的 ,均有
,均有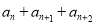 为定值.若
为定值.若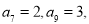
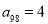 ,则数列
,则数列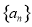 的前100项的和
的前100项的和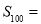 ( ).
( ). 满足
满足 ,
, ,
, ,那么
,那么 ____.
____. )如图所示,则该棱锥的体积等于
)如图所示,则该棱锥的体积等于  。
。