题目内容
6.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{6}$,且$\overrightarrow a•\overrightarrow b=\sqrt{3}$,则$|\overrightarrow a-\overrightarrow b|$的最小值为$\sqrt{3}$-1.分析 根据条件进行数量积的运算得到$|\overrightarrow{a}||\overrightarrow{b}|=2$,可考虑求$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}$的范围,从而便有$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}-2\sqrt{3}$$≥4-2\sqrt{3}$,这样便可得出$|\overrightarrow{a}-\overrightarrow{b}|$的范围,从而得出$|\overrightarrow{a}-\overrightarrow{b}|$的最小值.
解答 解:根据条件:$|\overrightarrow{a}||\overrightarrow{b}|cos\frac{π}{6}=\sqrt{3}$;
∴$|\overrightarrow{a}||\overrightarrow{b}|=2$;
∴$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}={\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=$|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}-2\sqrt{3}≥2|\overrightarrow{a}||\overrightarrow{b}|-2\sqrt{3}$=$4-2\sqrt{3}$=$(\sqrt{3}-1)^{2}$,当|$\overrightarrow{a}$|=$|\overrightarrow{b}|=\sqrt{2}$时取“=”;
∴$|\overrightarrow{a}-\overrightarrow{b}|≥\sqrt{3}-1$;
∴$|\overrightarrow{a}-\overrightarrow{b}|$的最小值为$\sqrt{3}-1$.
故答案为:$\sqrt{3}-1$.
点评 考查数量积的运算及其计算公式,对不等式a2+b2≥2ab的应用,注意判断等号能否取到,完全平方公式的运用.

 阅读快车系列答案
阅读快车系列答案| A. | 6 | B. | 12 | C. | 24 | D. | 36 |
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
| A. | ($\frac{e^2}{4}$,+∞) | B. | ($\frac{{{e^{\;}}}}{2}$,+∞) | C. | (1,$\frac{e^2}{4}$) | D. | (1,$\frac{{{e^{\;}}}}{2}$) |
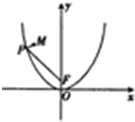 已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.
已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.