题目内容
给定两个长度为1的平面向量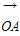 和
和 ,它们的夹角为90°,如图所示,点C在以O为圆心的圆弧AB上运动,若
,它们的夹角为90°,如图所示,点C在以O为圆心的圆弧AB上运动,若 =x
=x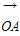 +y
+y ,其中x,y∈R,则x+y的最大值是( )
,其中x,y∈R,则x+y的最大值是( )
A.1 B.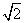
C. D.2
D.2

B
[解析] 方法一:以O为原点,向量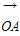 ,
, 所在直线分别为x轴,y轴建立直角坐标系,设〈
所在直线分别为x轴,y轴建立直角坐标系,设〈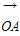 ,
,
 ∴x+y=cosθ+sinθ=
∴x+y=cosθ+sinθ=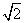 sin(θ+
sin(θ+ ),
),
又θ+ ∈[
∈[ ,
, ],
],
∴x+y的最大值为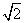 .
.
方法二:因为点C在以O为圆心的圆弧AB上,
所以| |2=|x
|2=|x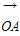 +y
+y |2=x2+y2+2xy
|2=x2+y2+2xy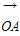 ·
· =x2+y2=1≥
=x2+y2=1≥ .所以x+y≤
.所以x+y≤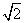 ,当且仅当x=y=
,当且仅当x=y= 时等号成立.
时等号成立.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 =
= ,
, =3,则△ABC的面积为________.
=3,则△ABC的面积为________. (λ∈R),则λ的值为________.
(λ∈R),则λ的值为________. ,
, ) B.(-
) B.(- =(2,2).若∠ABO=90°,则实数t的值为________.
=(2,2).若∠ABO=90°,则实数t的值为________. =( )
=( )
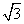 B.
B.
 D.
D.