题目内容
12.已知命题p:x2-8x-20≤0,命题q:(x-1-m)(x-1+m)≤0(m>0);若q是p的充分而不必要条件,求实数m的取值范围.分析 分别解出不等式,利用q是p的充分而不必要条件即可得出.
解答 解:命题p:x2-8x-20≤0,解得:-2≤x≤10.
命题q:(x-1-m)(x-1+m)≤0(m>0),解得:1-m≤x≤1+m.
若q是p的充分而不必要条件,∴$\left\{\begin{array}{l}{-2≤1-m}\\{1+m≤10}\end{array}\right.$,解得m≤3.
∴实数m的取值范围是(-∞,3].
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
7.函数y=2x(x≤0)的值域是( )
| A. | (0,1) | B. | (-∞,1) | C. | (0,1] | D. | [0,1) |
10.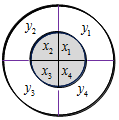 已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1,x2,x3,x4,大圆盘上所写的实数分别记为y1,y2,y3,y4,如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90°,记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( )
已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1,x2,x3,x4,大圆盘上所写的实数分别记为y1,y2,y3,y4,如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90°,记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( )
 已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1,x2,x3,x4,大圆盘上所写的实数分别记为y1,y2,y3,y4,如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90°,记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( )
已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1,x2,x3,x4,大圆盘上所写的实数分别记为y1,y2,y3,y4,如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90°,记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( )| A. | T1,T2,T3,T4中至少有一个为正数 | B. | T1,T2,T3,T4中至少有一个为负数 | ||
| C. | T1,T2,T3,T4中至多有一个为正数 | D. | T1,T2,T3,T4中至多有一个为负数 |
 如图是4为评委给某作品打出的分数的茎叶图,那么4为评委打出的分数的方差是$\frac{5}{2}$.
如图是4为评委给某作品打出的分数的茎叶图,那么4为评委打出的分数的方差是$\frac{5}{2}$.