题目内容
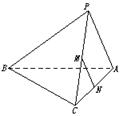
在Rt△ABC中,∠ACB=30°,∠B=90°,D为AC中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角A-BD-C大小记为θ.
(Ⅰ)求证:面AEF⊥面BCD;
(Ⅱ)θ为何值时,AB⊥CD.
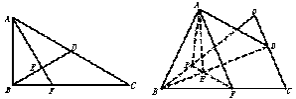
(Ⅰ)求证:面AEF⊥面BCD;
(Ⅱ)θ为何值时,AB⊥CD.
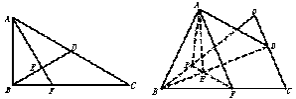
见解析
(Ⅰ)证明:在Rt△ABC中,∠C=30°,D为AC的中点,则△ABD是等边三角形
又E是BD的中点,∵BD⊥AE,BD⊥EF,折起后,AE∩EF=E,∴BD⊥面AEF
∵BD 面BCD,∴面AEF⊥面BCD
面BCD,∴面AEF⊥面BCD
(Ⅱ)解:过A作AP⊥面BCD于P,则P在FE的延长线上,设BP与CD相交于Q,
令AB=1,则△ABD是边长为1的等边三角形,若AB⊥CD,则BQ⊥CD

由于∠AEF=θ就是二面角A-BD-C的平面角,

又E是BD的中点,∵BD⊥AE,BD⊥EF,折起后,AE∩EF=E,∴BD⊥面AEF
∵BD
 面BCD,∴面AEF⊥面BCD
面BCD,∴面AEF⊥面BCD (Ⅱ)解:过A作AP⊥面BCD于P,则P在FE的延长线上,设BP与CD相交于Q,
令AB=1,则△ABD是边长为1的等边三角形,若AB⊥CD,则BQ⊥CD

由于∠AEF=θ就是二面角A-BD-C的平面角,


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
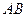
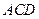
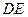
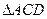
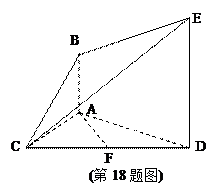
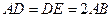 ,且
,且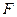 是
是 的中点.
的中点.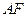 ∥平面
∥平面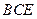 ;
;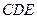 .
.
 中,求证:平面
中,求证:平面 平面
平面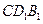 .
.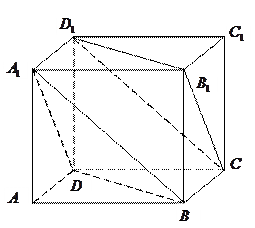
 的重心
的重心 ,作
,作 面
面 .
. 和△
和△ 都是直角三角形.
都是直角三角形.
 在平面
在平面 内,则直线
内,则直线