题目内容
已知定义在R上的函数f(x)满足对任意的x∈R都有f(1-x)=f(1+x),且f(x)在区间[0,1]上为增函数,则f(
) f(
)(用“>或<”填空).
| 1 |
| 2 |
| 7 |
| 4 |
考点:函数单调性的性质
专题:计算题,函数的性质及应用
分析:由f(1-x)=f(1+x),可得f(
)=f(
),再利用函数的单调性得f(
)>f(
),进而可得答案.
| 7 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:由f(1-x)=f(1+x),得f(
)=f(1+
)=f(1-
)=f(
),
∵f(x)在区间[0,1]上为增函数,
∴f(
)>f(
),即f(
)>f(
),
故答案为:>.
| 7 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
∵f(x)在区间[0,1]上为增函数,
∴f(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
故答案为:>.
点评:该题考查函数的单调性、对称性及其应用,属基础题,正确理解函数的相关性质是解题关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )

| A、2 | B、3 | C、4 | D、5 |
在等差数列{an}中,a1+3a8+a15=120,则2a6-a4的值为( )
| A、24 | B、22 | C、20 | D、-8 |
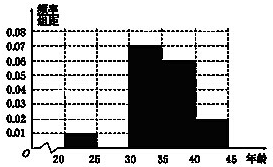 对某项活动中800名青年志愿者的年龄抽样调查后,得到如图所示的频率分布直方图,但年龄在25,30)的数据不慎丢失.依据此图,估计该项活动中年龄在25,30)的志愿者人数为
对某项活动中800名青年志愿者的年龄抽样调查后,得到如图所示的频率分布直方图,但年龄在25,30)的数据不慎丢失.依据此图,估计该项活动中年龄在25,30)的志愿者人数为