题目内容
如图，在△ABC中，D是BC上的一点．已知∠B=60°，AD=2，AC=
，DC=
，则AB= ．
| 10 |
| 2 |
考点：解三角形的实际应用
专题：综合题,解三角形
分析：利用余弦定理求出∠ADB=45°，再利用正弦定理，即可求出AB．
解答：
解：由题意，cos∠ADC=
=-
，
∴∠ADC=135°，
∴∠ADB=45°，
∵∠B=60°，AD=2，
∴
=
，
∴AB=
，
故答案为：
．
| 4+2-10 | ||
2×2×
|
| ||
| 2 |
∴∠ADC=135°，
∴∠ADB=45°，
∵∠B=60°，AD=2，
∴
| 2 | ||||
|
| AB | ||||
|
∴AB=
2
| ||
| 3 |
故答案为：
2
| ||
| 3 |
点评：本题考查正弦定理、余弦定理的运用，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0）的左、右焦点分别为F1，F2，P为双曲线上任一点，且
•
最小值的取值范围是[-
c2，-
c2]，则该双曲线的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 3 |
| 4 |
| 1 |
| 2 |
A、(1，
| ||
B、[
| ||
C、(1，
| ||
| D、[2，+∞） |
已知关于x的方程|x2-2x|=a（a＞0）的解集为P，则P中所有元素的和可能是（ ）
| A、1，2，3 |
| B、2，3，4 |
| C、3，4，5 |
| D、2，3，5 |
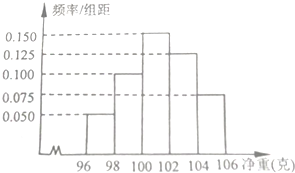某工厂为了了解一批产品的净重（单位：克）情况，从中随机抽测了100件产品的净重，所得数据均在区间[96，106]中，其频率分布直方图如图所示，则在抽测的100件产品中，净重在区间[100，104]上的产品件数是某种树的分枝生长规律如图所示，则预计到第6年树的分枝数为（ ）
| A、5 | B、6 | C、7 | D、8 |
已知i是虚数单位，则
=（ ）
| i |
| 1-i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|