题目内容
分解因式：
（1）5x2-15x+2xy-6y
（2）3a3b-81b4
（3）-a4+16．
（1）5x2-15x+2xy-6y
（2）3a3b-81b4
（3）-a4+16．
考点：因式分解定理
专题：计算题
分析：（1）分组提取公因式5x，再提取公因式x-3即可；
（2）先提取公因式3b，再利用立方差公式即可；
（3）利用平方差公式展开即可．
（2）先提取公因式3b，再利用立方差公式即可；
（3）利用平方差公式展开即可．
解答：
解：（1）原式=5x（x-3）+2y（x-3）=（x-3）（5x+2y），
（2）原式=3b[a3-（3b）3]=3b（a-3b）（a2+9b2-3ab）．
（3）原式=-（a4-24）=-（a2+4）（a-2）（a+2）．
（2）原式=3b[a3-（3b）3]=3b（a-3b）（a2+9b2-3ab）．
（3）原式=-（a4-24）=-（a2+4）（a-2）（a+2）．
点评：本题考查了提取公因式、立方差公式、平方差公式法分解因式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图是“集合”的知识结构图，如果要加入“子集”，则应放在（ ）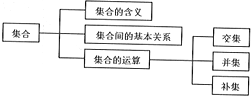
| A、“集合的含义”的下位 |
| B、“集合间的基本关系”的下位 |
| C、“交集”的下位 |
| D、“集合的运算”的下位 |
y=2sin（x+
），x∈[0，
]．最大值 为（ ）
| π |
| 3 |
| π |
| 2 |
| A、1 | ||
B、
| ||
| C、-2 | ||
| D、2 |