Question

6．在周长为6的△ABO中，∠AOB=60°，点P在边AB上，PH⊥OA于H（点H在边OA上），且PH=$\frac{\sqrt{3}}{2}$，OP=$\frac{\sqrt{7}}{2}$．则边OA的长为2.1．

Answer 1

分析 先求出HC=1，BO，再过O作OQ⊥AB于Q，求出BQ，AQ，利用周长为6，即可得出结论．

解答 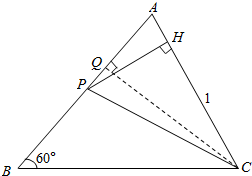解：∵PH=$\frac{\sqrt{3}}{2}$，OP=$\frac{\sqrt{7}}{2}$，
∴HC=1，
设AH=x，则AO=x+1，AP=$\sqrt{{x}^{2}+\frac{3}{4}}$，
sinA=$\frac{\frac{\sqrt{3}}{2}}{\sqrt{{x}^{2}+\frac{3}{4}}}$，
由正弦定理，可得BO=$\frac{2（x+1）}{\sqrt{4{x}^{2}+3}}$．
过O作OQ⊥AB于Q，
∴BQ=$\frac{x+1}{\sqrt{4{x}^{2}+3}}$，AQ=$\frac{2x（x+1）}{\sqrt{4{x}^{2}+3}}$，
∵周长为6，
∴$\frac{2（x+1）}{\sqrt{4{x}^{2}+3}}$+$\frac{x+1}{\sqrt{4{x}^{2}+3}}$+$\frac{2x（x+1）}{\sqrt{4{x}^{2}+3}}$+x+1=6
∴（x²+1）（60x-66）=0，
∴x=1.1，
∴AO=2.1，
故答案为：2.1．

点评 本题考查正弦定理，考查三角形周长的计算，考查学生分析解决问题的能力，属于中档题．