题目内容
已知f（x）=x2+x．求f（a+
）的最小值．
| 1 |
| a |
考点：二次函数的性质,基本不等式
专题：函数的性质及应用
分析：通过讨论a的范围，结合基本不等式的性质从而得到答案．
解答：
解：∵f（x）=x2+x=(x+
)2-
，
∴f（a+
）=(a+
+
)2-
当a＞0时，f（a+
）≥
-
=6，当且仅当a=1时“=”成立，
当a＜0时，f（a+
）≥
-
=2，当且仅当a=-1时“=”成立．
| 1 |
| 2 |
| 1 |
| 4 |
∴f（a+
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| 4 |
当a＞0时，f（a+
| 1 |
| a |
| 25 |
| 4 |
| 1 |
| 4 |
当a＜0时，f（a+
| 1 |
| a |
| 9 |
| 4 |
| 1 |
| 4 |
点评：本题考查了二次函数的性质，考查了基本不等式的性质，是一道基础题．
练习册系列答案
相关题目
若一个底面是正三角形的三棱柱的主视图如图所示，则其表面积为（ ）
A、6+2
| ||
B、6+
| ||
C、6+4
| ||
| D、10 |
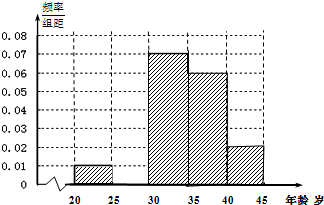某市要对两千多名出租车司机的年龄进行调查，现从中随机抽出100名司机，已知抽到的司机年龄都在[20，45）岁之间，根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是
某公司组织结构如表，其中销售部的直接领导是（ ）
| A、副总经理（甲） |
| B、副总经理（乙） |
| C、总经理 |
| D、董事会 |