题目内容
某几何体三视图如图所示,则该几何体的体积为


考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由已知中的三视图可得,该几何体是一个以俯视图为底面的柱体,求出底面面积和高,代入柱体体积公式,可得答案.
解答:
解:由已知中的三视图可得,该几何体是一个以俯视图为底面的柱体,
柱体的底面面积S=2×2-1×1-
π=3-
,
由柱体的高为h=2,
故该几何体的体积V=Sh=6-
.
故答案为:6-
.
柱体的底面面积S=2×2-1×1-
| 1 |
| 4 |
| π |
| 4 |
由柱体的高为h=2,
故该几何体的体积V=Sh=6-
| π |
| 2 |
故答案为:6-
| π |
| 2 |
点评:本题考查的知识点是由三视图求体积,其中分析出几何体的形状,是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
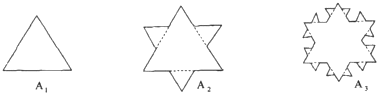
设有一个边长为3的正三角形,记为A1,将A1的每边三等份,在中间的线段上向图形外作正三角形,去掉中间的线段后所得到的图形记为A2;将A2的每边三等份,再重复上述过程,得到图形A3;再重复上述过程,得到图形A4,则A4的周长是( )

| A、12 | ||
| B、16 | ||
C、
| ||
D、
|
一个球的体积是
π,这个球的半径等于( )
| 32 |
| 3 |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、2π |
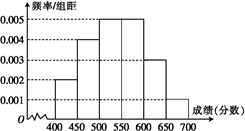 为对考生的月考成绩进行分析,某地区随机抽查了10000名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
为对考生的月考成绩进行分析,某地区随机抽查了10000名考生的成绩,根据所得数据画了如下的样本频率分布直方图.