题目内容
数列{an}中满足a1=1,且对于任意的正整数都有an+1=an+n,则
= .
| 1 |
| an |
考点:数列递推式
专题:等差数列与等比数列
分析:对于任意的正整数都有an+1=an+n,利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=(n-1)+(n-2)+…+2+1+1即可得出.
解答:
解:∵对于任意的正整数都有an+1=an+n,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(n-1)+(n-2)+…+2+1+1
=
+1=
.
∴
=
.
故答案为:
.
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(n-1)+(n-2)+…+2+1+1
=
| (n-1)n |
| 2 |
| n2-n+2 |
| 2 |
∴
| 1 |
| an |
| 2 |
| n2-n+2 |
故答案为:
| 2 |
| n2-n+2 |
点评:本题考查了“累加求和”、等差数列的前n项和公式,考查了计算能力,属于基础题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
如图,设全集U=N,集合A={1,3,5,7,8},B={1,2,3,4,5},则图中阴影部分表示的集合为( 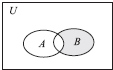

| A、{2,4} |
| B、{7,8} |
| C、{1,3,5} |
| D、{1,2,3,4,5} |
曲线y=xe2x-1在点(1,e)处切线的斜率等于( )
| A、2e | B、e | C、3e | D、1 |