题目内容
11．已知集合M={x|x2-2x≥0}，N={x|x≤1}，则（∁RM）∩N={x|0＜x≤1}．分析 先求解一元二次不等式化简集合M，求出∁RM，则（∁RM）交N的答案可求．
解答 解：集合M={x|x2-2x≥0}={x|x≤0，或x≥2}，
∴∁RM={x|0＜x＜2}，
∵N={x|x≤1}，
∴（∁RM）∩N={x|0＜x≤1}，
故答案为：{x|0＜x≤1}．
点评 本题考查了交、并、补集的混合运算，是基础题．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
1．某公司为确定明年投入某产品广告支出，对近5年的广告支出m与销售额t（单位：百万元）进行了初步统计，得到下列表格中的数据：
经测算，年广告支出m和年销售额t满足线性回归方程$\widehat{t}$=6.5m+17.5，则p的值为60．
| t | 30 | 40 | p | 50 | 70 |
| m | 2 | 4 | 5 | 6 | 8 |
2．设点P是△ABC所在平面内的一点，$\overrightarrow{PA}$+2$\overrightarrow{PB}$+3$\overrightarrow{PC}$=4$\overrightarrow{AB}$，且△ABC的面积为S，则下列判断正确的是（ ）
| A． | 点P在△ABC外，且△APC的面积为$\frac{1}{3}$S | B． | 点P在△ABC外，且△APC的面积为$\frac{1}{2}$S | ||
| C． | 点P在△ABC内，且△APC的面积为$\frac{1}{3}$S | D． | 点P在△ABC内，且△APC的面积为$\frac{1}{2}$S |
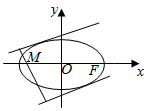已知点F（1，0）是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦点，且椭圆C上的点到点F的最大距离为$\sqrt{2}+1$．