题目内容
已知点P在焦点为F1和F2的椭圆
+
=1上，若∠F1PF2=90°，求|PF1|•|PF2|的值．
| x2 |
| 45 |
| y2 |
| 20 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据椭圆的定义和勾股定理建立关于m、n的方程组，平方相减即可求|PF1|•|PF2|，得到本题答案．
解答：
解：∵椭圆方程
+
=1，
∴a2=45，b2=20，可得c2=a2-b2=25，即a=3
，c=5，
设|PF1|=m，|PF2|=n，
∵∠F1PF2=90°得PF1⊥PF2，则有
，
即（m+m）2=m2+n2+2mn，
则180=100+2mn
得2mn=80，即mn=40，
∴|PF1|•|PF2|=40．
|PF1|•|PF2|的值：40．
| x2 |
| 45 |
| y2 |
| 20 |
∴a2=45，b2=20，可得c2=a2-b2=25，即a=3
| 5 |
设|PF1|=m，|PF2|=n，
∵∠F1PF2=90°得PF1⊥PF2，则有
|
即（m+m）2=m2+n2+2mn，
则180=100+2mn
得2mn=80，即mn=40，
∴|PF1|•|PF2|=40．
|PF1|•|PF2|的值：40．
点评：本题给出椭圆的焦点三角形为直角三角形，求它的面积，着重考查了勾股定理、椭圆的定义和简单几何性质等知识．
练习册系列答案
相关题目
将指数形式256=2x化为对数形式，下列结果正确的是（ ）
| A、log2256=8 |
| B、log2562=8 |
| C、log8256=2 |
| D、log2568=2 |
已知A，B，C是直线l上的三点，向量
，
，
满足
=[f（x）+2f′（1）x]
-lnx•
，则函数y=f（x）的表达式是（ ）
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
A、f（x）=lnx-
| ||
B、f（x）=lnx-
| ||
| C、f（x）=lnx+2x+1 | ||
| D、f（x）=lnx+2x |
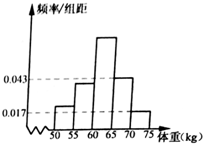某校为了解2015届高三毕业班准备考飞行员学生的身体素质，对他们的体重进行了测量，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右前3个小组的频率之比为1：2：4，其中第二小组的频率为11．