题目内容
7.M是椭圆$\frac{x^2}{9}+{y^2}=1$上动点,F1,F2是椭圆的两焦点,则∠F1MF2的最大值为π-arccos$\frac{7}{9}$.分析 求得椭圆的a,b,c,由椭圆中焦点三角形中,焦距所对角最大,可得∠F1MF2最大,此时M为短轴端点.再由余弦定理,计算即可得到所求最大角.
解答 解:椭圆$\frac{x^2}{9}+{y^2}=1$的a=3,b=1,c=$\sqrt{{a}^{2}-{b}^{2}}$=2$\sqrt{2}$,
由椭圆中焦点三角形中,焦距所对角最大,
可得∠F1MF2最大,此时M为短轴端点.
则cos∠F1MF2=$\frac{|M{F}_{1}{|}^{2}+|M{F}_{2}{|}^{2}-|{F}_{1}{F}_{2}{|}^{2}}{2|M{F}_{1}||M{F}_{2}|}$
=$\frac{9+9-4×8}{2×9×9}$=-$\frac{7}{9}$,
可得∠F1MF2的最大值为π-arccos$\frac{7}{9}$.
故答案为:π-arccos$\frac{7}{9}$.
点评 本题考查椭圆的方程和性质,注意最大角原理,考查运算能力,属于基础题.

练习册系列答案
相关题目
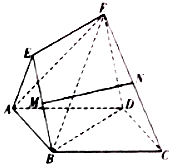 如图5所示,四边形ABCD是边长为2的正方形,四边形BDFE是平行四边形,点M,N分别是BE,CF的中点.
如图5所示,四边形ABCD是边长为2的正方形,四边形BDFE是平行四边形,点M,N分别是BE,CF的中点.