题目内容
10. 如图直三棱柱ABC-A1B1C1 中AC=2AA1,AC⊥BC,D、E 分别为A1C1、AB 的中点.求证:
如图直三棱柱ABC-A1B1C1 中AC=2AA1,AC⊥BC,D、E 分别为A1C1、AB 的中点.求证:(1)AD⊥平面BCD
(2)A1E∥平面BCD.
分析 (1)只需证明BC⊥AD,DC⊥AD,证明 即可AD⊥平面BCD
(2)取BC中点O,连结DO、OE可得四边形A1DOE为平行四边形,即A1E∥OD,A1E∥平面BCD.
解答 证明:(1)∵直三棱柱ABC-A1B1C1中CC1⊥平面ABC,又BC?平面ABC,
∴CC1⊥BC,
又∵AC⊥BC,AC∩CC1=C,AC,CC1?平面AA1C1C,
∴BC⊥平面AA1C1C,
而AD?平面AA1C1C∴BC⊥AD…①
又该直三棱柱中AA1⊥A1C1,CC1⊥A1C1,
由已知AA1=$\frac{1}{2}$ AC=A1D,则∠A1DA=$\frac{π}{4}$,
同理∠C1DC=$\frac{π}{4}$,则∠ADC=$\frac{π}{2}$,即CD⊥AD,
由①BC⊥AD,BC∩CD=C,BC,CD?平面BCD,
∴AD⊥平面BCD;
(2)取BC中点O,连结DO、OE,∵AE=EB,CO=BO∴OE平行等于$\frac{1}{2}$ AC,
而A1D平行等于$\frac{1}{2}$AC,
∴A1D平行等于OE∴四边形A1DOE为平行四边形,
∴A1E∥OD,而A1E?平面BCD,OD?平面BCD,
∴A1E∥平面BCD.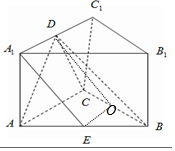
点评 本题考查了空间线面垂直、线面平行的判定,属于中档题

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
18.已知A是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点,F1,F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若$\overrightarrow{GA}$=λ$\overrightarrow{P{F}_{1}}$,|$\overrightarrow{GA}$|=$\frac{5}{3}$,|$\overrightarrow{P{F}_{1}}$|+|$\overrightarrow{P{F}_{2}}$|=8,则双曲线的标准方程为( )
| A. | x2-$\frac{{y}^{2}}{8}$=1 | B. | $\frac{{x}^{2}}{16}$-y2=1 | C. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}$=1 | D. | x2-$\frac{{y}^{2}}{4}$=1 |
15.设集合A={x|y=log2(x-1)},$B=\{y|y=\sqrt{2-x}\}$,则A∩B=( )
| A. | (0,2] | B. | (1,2) | C. | (1,+∞) | D. | (1,2] |
19.已知函数f(x)=x-ex(e为自然对数的底数),g(x)=mx+1,(m∈R),若对于任意的x1∈[-1,2],总存在x0∈[-1,1],使得g(x0)=f(x1) 成立,则实数m的取值范围为( )
| A. | (-∞,-e]∪[e,+∞﹚ | B. | [-e,e] | ||
| C. | ﹙-∞,-2-$\frac{1}{e}$]∪[-2+$\frac{1}{e}$,+∞﹚ | D. | [-2-$\frac{1}{e}$,-2+$\frac{1}{e}$] |
4.对同一目标进行三次射击,第一、二、三次射击命中目标的概率分别为0.4,0.5和0.7,则三次射击中恰有一次命中目标的概率是( )
| A. | 0.36 | B. | 0.64 | C. | 0.74 | D. | 0.63 |
 函数f(x)与g(x)的定义域为[m,n],它们的图象如图所示,则不等式f(x)g(x)<0的解集是{x|x∈(m,a)∪(a,b)∪(c,d)}.
函数f(x)与g(x)的定义域为[m,n],它们的图象如图所示,则不等式f(x)g(x)<0的解集是{x|x∈(m,a)∪(a,b)∪(c,d)}. 如图,四边形ABCD与BDEF均为边长为2的菱形,∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF均为边长为2的菱形,∠DAB=∠DBF=60°,且FA=FC.