题目内容
6．在△ABC中，若AB=2，AC=3，∠A=60°，则BC=$\sqrt{7}$； 若AD⊥BC，则AD=$\frac{3\sqrt{21}}{7}$．分析 利用余弦定理求BC，利用面积公式求出AD．
解答 解：∵AB=2，AC=3，∠A=60°，
∴由余弦定理可得BC=$\sqrt{4+9-2×2×3×\frac{1}{2}}$=$\sqrt{7}$，
$\frac{1}{2}×2×3×sin60°$=$\frac{1}{2}•\sqrt{7}•AD$，∴AD=$\frac{3\sqrt{21}}{7}$，
故答案为$\sqrt{7}$，$\frac{3\sqrt{21}}{7}$．
点评 本题考查余弦定理、三角形面积公式，考查学生的计算能力，属于中档题．
练习册系列答案
天天练口算系列答案
相关题目
6．某校高三共有男生400名，从所有高三男生中随机抽取20名男生测量身高（单位：cm）作为样本，得到频率分布表与频率分布直方图1（部分）如表：
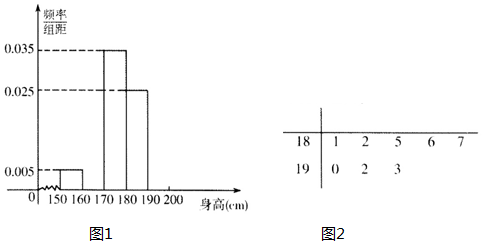
（Ⅰ）求n1、n2、f1、f2；
（Ⅱ）试估计身高不低于180cm的该校高三男生人数，并说明理由；
（Ⅲ）从样本中不低于180cm的男生身高，绘制成茎叶图（图2）；
现从身高不低于185cm的男生中任取3名参加选拔性测试，求至少有两位身高不低于190cm的概率．
| 分组 | 频数 | 频率 |
| [150，160） | 1 | |
| [160，170） | n1 | f1 |
| [170，180） | n2 | f2 |
| [180，190） | 5 | |
| [190，200] | 3 |
（Ⅰ）求n1、n2、f1、f2；
（Ⅱ）试估计身高不低于180cm的该校高三男生人数，并说明理由；
（Ⅲ）从样本中不低于180cm的男生身高，绘制成茎叶图（图2）；
现从身高不低于185cm的男生中任取3名参加选拔性测试，求至少有两位身高不低于190cm的概率．
11．在（1-x）5+（1-x）6+（1-x）7+（1-x）8的展开式中，含x3的项的系数是（ ）
| A． | 121 | B． | -74 | C． | 74 | D． | -121 |
15．
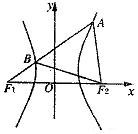如图，F1，F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点，过F1的直线l与双曲线分别交于点A，B，若△ABF2为等边三角形，则双曲线的渐近线的斜率为（ ）
如图，F1，F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点，过F1的直线l与双曲线分别交于点A，B，若△ABF2为等边三角形，则双曲线的渐近线的斜率为（ ）| A． | ±$\sqrt{3}$ | B． | ±2 | C． | $±\sqrt{6}$ | D． | ±$\sqrt{2}$ |
16．若扇形的圆心角为$\frac{2}{3}$π弧度，r=2，则扇形的面积是（ ）
| A． | $\frac{8}{3}$π | B． | $\frac{4}{3}$ | C． | $\frac{3}{2}π$ | D． | $\frac{4}{3}$π |