题目内容
2.已知正三棱锥P-ABC中所有顶点都在球O表面上,PA,PB,PC两两互相垂直,若三棱锥P-ABC体积是$\frac{4}{3}$,则球O的表面积是12π.分析 由V=$\frac{1}{3}×\frac{1}{2}×PA×PB×PC$=$\frac{4}{3}$,得PA=PB=PC=2
正三棱锥P-ABC的外接球,就是以PA为棱长的正方体的外接球,故球的半径为R=$\frac{1}{2}×\sqrt{{2}^{2}+{2}^{2}+{2}^{2}}=\sqrt{3}$即可求得球O的表面积.
解答 解:正三棱锥P-ABC中,PA,PB,PC两两互相垂直,三棱锥P-ABC体积是$\frac{4}{3}$,则V=$\frac{1}{3}×\frac{1}{2}×PA×PB×PC$=$\frac{4}{3}$,
∵PA=PB=PC,∴PA=PB=PC=2,
正三棱锥P-ABC的外接球,就是以PA为棱长的正方体的外接球,故球的半径为R=$\frac{1}{2}×\sqrt{{2}^{2}+{2}^{2}+{2}^{2}}=\sqrt{3}$,
∴球O的表面积s=4πR2=12π,
故答案为:12π.
点评 本题给出三棱锥的三条侧棱两两垂直,求它的外接球的表面积,着重考查了长方体对角线公式和球的表面积计算等知识,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
10.方程$(x+y-1)\sqrt{{x^2}+{y^2}-4}=0$所表示的图形是( )
| A. | 两条射线及一个圆 | B. | 两个点 | ||
| C. | 一条线段及一个圆 | D. | 一条直线及一个圆 |
17.已知数列{an}的前n项和Sn=n2an(n≥2),而a1=1,通过计算a2,a3,猜想an等于( )
| A. | $\frac{2}{{{{(n+1)}^2}}}$ | B. | $\frac{2}{n(n+1)}$ | C. | $\frac{1}{{{2^n}-1}}$ | D. | $\frac{1}{2n-1}$ |
11.某程序框图如图所示,运行该程序输出的k值是( )
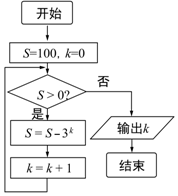

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.已知一个数列的前n项和为Sn=3n2+2n+5,则它的第n(n≥2)项为( )
| A. | 3n2 | B. | 3n2+3n | C. | 6n+1 | D. | 6n-1 |
 如图,已知四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD
如图,已知四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD 随着智能手机的普及,网络购物越来越受到人们的青睐,某研究性学习小组对使用智能手机的利与弊随机调查了10位同学,得到的满意度打分如茎叶图所示.若这组数据的中位数、平均数分别为a,b,则a,b的大小关系是a=b.
随着智能手机的普及,网络购物越来越受到人们的青睐,某研究性学习小组对使用智能手机的利与弊随机调查了10位同学,得到的满意度打分如茎叶图所示.若这组数据的中位数、平均数分别为a,b,则a,b的大小关系是a=b.