题目内容
5.已知函数f(x)=$\sqrt{3}$sinxcosx的图象与函数g(x)=3sin2x-λ(λ∈R)的图象在$[{-\frac{π}{4},\frac{π}{2}}]$上有两个交点,则实数λ的取值范围是( )| A. | $(\frac{{3-2\sqrt{3}}}{2},0]$ | B. | $(\frac{{3-2\sqrt{3}}}{2},3]$ | C. | $(\frac{{3-2\sqrt{3}}}{2},\frac{{3+2\sqrt{3}}}{2}]$ | D. | $(\frac{{3-2\sqrt{3}}}{2},\frac{{3+2\sqrt{3}}}{2}]$ |
分析 由题意,令函数F(x)=f(x)-g(x),f(x)和g(x)交点问题转化为F(x)的零点问题,又令F(x)=0转化为三角函数图象与直线的交点问题,在$[{-\frac{π}{4},\frac{π}{2}}]$上求出三角函数的值域,利用图象可得解.
解答 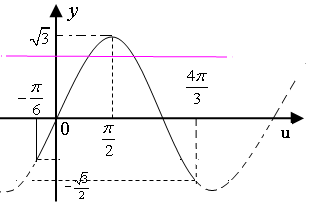 解:由题意,令函数F(x)=f(x)-g(x),
解:由题意,令函数F(x)=f(x)-g(x),
即F(x)=$\sqrt{3}$sinxcosx-3sin2x+λ=$\frac{\sqrt{3}}{2}$sin2x+$\frac{3}{2}$cos2x+λ$-\frac{3}{2}$=$\sqrt{3}$sin(2x+$\frac{π}{3}$)+λ$-\frac{3}{2}$.
要求F(x)的零点,令F(x)=0,可得$\sqrt{3}$sin(2x+$\frac{π}{3}$)+λ$-\frac{3}{2}$=0.
转化为函数y=$\sqrt{3}$sin(2x+$\frac{π}{3}$)与y=$\frac{3}{2}-λ$图象的交点问题.
当x在$[{-\frac{π}{4},\frac{π}{2}}]$上时,
令2x+$\frac{π}{3}$=u,
则:u∈[$-\frac{π}{6}$,$\frac{4π}{3}$].
可得y=$\sqrt{3}$sinu的图象如下:
从图象看出:$-\frac{1}{2}×\sqrt{3}$≤$\frac{3}{2}-λ$$<\sqrt{3}$时,图象由两个交点,
∴$-\frac{2+\sqrt{3}}{2}≤$-λ<$\frac{2\sqrt{3}-3}{2}$.
故选:C.
点评 本题考查了三角函数交点的问题,转化为令函数零点的问题,构造成新函数,利用图象求解,属于中档题.

练习册系列答案
相关题目
15.已知二次函数f(x)=x2+bx+c的两个零点分别在区间(-2,-1)和(-1,0)内,则f(3)的取值范围是( )
| A. | (12,20) | B. | (12,18) | C. | (18,20) | D. | (8,18) |
16.若x+x11=a0+a1(x+1)+a2(x+1)2+…+a10(x+1)10+a11(x+1)11,则a10的值为( )
| A. | 10 | B. | -10 | C. | -11 | D. | 11 |
20.设复数$z=\frac{2i}{cos120°+isin120°}$,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | 2 |
15. 如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )
如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )
 如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )
如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{\begin{array}{l}8\end{array}}$ | D. | $\frac{3}{4}$ |