题目内容
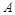
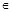 平面
平面 若
若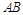 与
与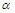 所成角正弦值为0.8,
所成角正弦值为0.8, 与
与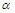 成450角,则
成450角,则 距离的范围( )
距离的范围( )
A.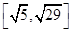 | B. |
C.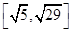 | D.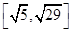 ∪ ∪ |
D.
解析试题分析:分两种情形.①若 在平面
在平面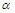 的同侧:如图(1)、图(2).
的同侧:如图(1)、图(2).

图(1) 图(2)
当 如图(1)位置时,在直角梯形
如图(1)位置时,在直角梯形 中
中 可求得
可求得 ;当
;当 如图(2)位置时,在直角梯形
如图(2)位置时,在直角梯形 中
中 可求得
可求得 .因此当
.因此当 在平面
在平面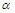 的同侧时,
的同侧时,
②若 在平面
在平面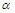 的两侧:如图(3)、图(4).
的两侧:如图(3)、图(4).

图(3) 图(4)
当 如图(3)位置时,在
如图(3)位置时,在 中
中 可求得
可求得 ;当
;当 如图(4)位置时,在
如图(4)位置时,在 中
中 可求得
可求得 .因此当
.因此当 在平面
在平面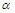 的两侧时,
的两侧时, 综上所述,
综上所述, 距离的范围为
距离的范围为 .
.
考点:1.空间线面角的计算;2.空间两点间距离.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
设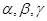 是三个互不重合的平面,
是三个互不重合的平面,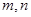 是两条不重合的直线,则下列命题中正确的是( )
是两条不重合的直线,则下列命题中正确的是( )
A.若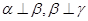 ,则 ,则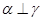 |
B.若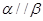 , ,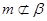 , ,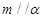 ,则 ,则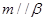 |
C.若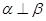 , ,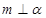 ,则 ,则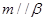 |
D.若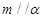 , ,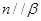 , ,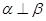 ,则 ,则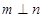 |
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
一个棱柱是正四棱柱的条件是( )
| A.底面是正方形,有两个侧面是矩形 |
| B.每个侧面都是全等矩形的四棱柱 |
| C.底面是菱形,且有一个顶点处的三条棱两两垂直 |
| D.底面是正方形,有两个相邻侧面垂直于底面 |
已知三条不重合的直线 ,两个不重合的平面
,两个不重合的平面 ,有下列命题:
,有下列命题:
①若 ,且
,且 ,则
,则
②若 ,且
,且 ,则
,则
③若 ,
, ,则
,则
④若 ,则
,则
其中真命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
如图,在正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中必有( )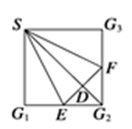
A.SG⊥△EF G所在平面 G所在平面 | B.SD⊥△EFG所在平面 |
C.GF ⊥△SEF所在平面 ⊥△SEF所在平面 | D.GD⊥△SEF所在平面 |
设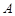 在
在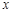 轴上,它到点
轴上,它到点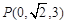 的距离等于到点
的距离等于到点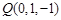 的距离的两倍,那么
的距离的两倍,那么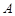 点的坐标是( )
点的坐标是( )
| A.(1,0,0)和( -1,0,0) | B.(2,0,0)和(-2,0,0) |
C.(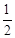 ,0,0)和( ,0,0)和(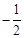 ,0,0) ,0,0) | D.(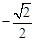 ,0,0)和( ,0,0)和( ,0,0) ,0,0) |
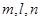 和平面
和平面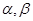 的四个命题:
的四个命题: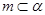 ,
,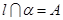 ,点
,点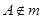 ,则
,则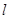 与
与 不共面;
不共面;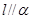 ,
,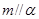 ,且
,且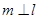 ,
, ,则
,则 ;
;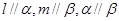 ,则
,则 ;
;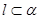 ,
,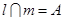 ,
, ,
, ,则
,则 .
.