题目内容
(2x-3y-1)7展开式中x2y3项的系数是 ;所有项系数和是 .
考点:二项式系数的性质
专题:二项式定理
分析:根据含x2y3项为
•(2x)2•(-3y)3•(-1)2=-2268x2y3,可得展开式中x2y3项的系数.在(2x-3y-1)7展开式中,令x=1可得所有项系数和.
| C | 2 7 |
解答:
解:由于(2x-3y-1)7展开式表示7个因式(2x-3y-1)的乘积,
从中任意选出2个因式取2x,3个因式取(-3y),还有2个因式取(-1),
形成即可得到x2y3项,故含x2y3项为
•(2x)2•(-3y)3•(-1)2=-2268x2y3,故展开式中x2y3项的系数是-2268.
在(2x-3y-1)7展开式中,令x=1可得所有项系数和是 (-2)7=-128,
故答案为:-2268;-128.
从中任意选出2个因式取2x,3个因式取(-3y),还有2个因式取(-1),
形成即可得到x2y3项,故含x2y3项为
| C | 2 7 |
在(2x-3y-1)7展开式中,令x=1可得所有项系数和是 (-2)7=-128,
故答案为:-2268;-128.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
相关题目
 如图,△ABC的外接圆的圆心为O,AB=3,AC=5,BC=
如图,△ABC的外接圆的圆心为O,AB=3,AC=5,BC=| 7 |
| AO |
| BC |
| A、-8 | B、-1 | C、1 | D、8 |
已知(1+x)6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6,则a1+a3+a5=( )
| A、-16 | B、0 | C、16 | D、32 |
在△ABC中,若cosBsinC=sinA,则△ABC的形状一定是( )
| A、等腰直角三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等边三角形 |
执行如图所示的程序框图,若输入n的值为4,则输出S的值为( )
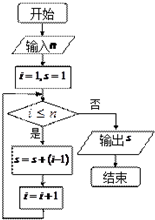

| A、5 | B、6 | C、7 | D、8 |