题目内容
如图所示的平面区域(阴影部分)满足的不等式为 .
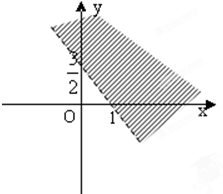

考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:求出直线方程,结合二元一次不等式与平面之间的关系即可得到结论.
解答:
解:直线方程为
+
=1,
即3x+2y-3=0,
当x=y=0时,0-3<0,
即原点在3x+2y-3<0的区域内,
则阴影部分的满足不等式为3x+2y-3>0,
故答案为:3x+2y-3>0
| x |
| 1 |
| y | ||
|
即3x+2y-3=0,
当x=y=0时,0-3<0,
即原点在3x+2y-3<0的区域内,
则阴影部分的满足不等式为3x+2y-3>0,
故答案为:3x+2y-3>0
点评:本题主要考查二元一次不等式表示平面区域,根据原点来定域是解决本题的关键.

练习册系列答案
相关题目
若sinA=
,则sin(6π-A)的值为( )
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f″(x)是f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心,设函数g(x)=
x3-
x2+3x-
,则g(
)+g(
)+…+g(
)=( )
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 2014 |
| 2015 |
| A、2 013 |
| B、2 014 |
| C、2 015 |
| D、2 016 |
已知集合M={x|y=
},N={x|y=log2(2-x)},则∁R(M∩N)=( )
| 2x-2 |
| A、[1,2) |
| B、(-∞,1)∪[2,+∞) |
| C、[0,1] |
| D、(-∞,0)∪[2,+∞) |