题目内容
如图,四棱锥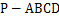 的底面
的底面 是平行四边形,
是平行四边形, ,
, ,
,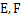 分别是棱
分别是棱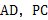 的中点.
的中点.
证明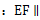 平面
平面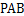 ;
;
若二面角P-AD-B为 ,
,
证明:平面PBC⊥平面ABCD
求直线EF与平面PBC所成角的正弦值.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
题目内容
如图,四棱锥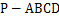 的底面
的底面 是平行四边形,
是平行四边形, ,
, ,
,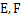 分别是棱
分别是棱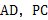 的中点.
的中点.
证明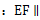 平面
平面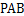 ;
;
若二面角P-AD-B为 ,
,
证明:平面PBC⊥平面ABCD
求直线EF与平面PBC所成角的正弦值.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案