题目内容
5.过椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点F2的直线与圆x2+y2=b2相切于点A,并与椭圆C交于不同的两点P,Q,若$\overrightarrow{PA}$=$\frac{1}{3}\overrightarrow{PQ}$,则椭圆离心率e=$\frac{\sqrt{5}}{3}$.分析 连接OA,PF1,则OA⊥PQ,得PF1⊥PQ,由A为线段PQ的靠近P的三等分点,得A为线段PA的中点,于是PF1=2b.结合椭圆的定义有PF2=2a-2b,由此能求出椭圆的离心率.
解答 解:如图,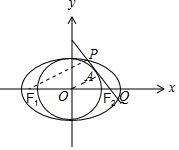
解:连接OA,PF1,
则OA⊥PQ,∴PF1⊥PQ,
∵$\overrightarrow{PA}$=$\frac{1}{3}\overrightarrow{PQ}$,∴A为线段PQ的靠近P的三等分点,则A为线段PF2的中点,
于是PF1=2b.
结合椭圆的定义有PF2=2a-2b,
在直角三角形PF1F2中,
利用勾股定理得(2a-2b)2+(2b)2=(2c)2,
将c2=a2-b2代入,
整理可得b=$\frac{2}{3}$a,
于是e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{{a}^{2}-\frac{4}{9}{a}^{2}}}{a}$=$\frac{\sqrt{5}}{3}$.
故答案为:$\frac{\sqrt{5}}{3}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,考查了数学转化思想方法,是中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
16.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆x2+y2=b2,若椭圆C上存在点P,使得过点P引圆O的两条切线,切点分别为A、B,满足∠APB=60°,则椭圆的离心率e的取值范围是( )
| A. | 0<e≤$\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$≤e<1 | C. | $\frac{\sqrt{3}}{2}$<e<1 | D. | $\frac{\sqrt{3}}{2}$≤e<1 |
13.执行如图的程序框图,如果输入的n是3,那么输出的p是( )


| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{24}$ | D. | $\frac{1}{120}$ |
14.下列各组函数是同一函数的是( )
| A. | y=$\frac{2x}{x}$与y=2 | B. | y=$\sqrt{{x}^{2}}$与y=($\sqrt{x}$)2 | C. | y=lgx2与y=2lgx | D. | y=$\frac{{x}^{2}}{x}$与y=x(x≠0) |
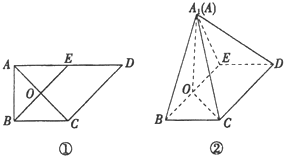 如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.
如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.