题目内容
6.某大型商场成立十周年之际,为了回馈顾客,特进行有奖销售:有奖销售期间,每购买满100元该商场的商品,都有一次抽奖机会,一旦中奖,将获得一个精美奖品;抽奖方案有A、B两种,可自主选择,A方案是:从装有3个红色小球和7个白色小球的箱子里每次摸1个小球,不放回地摸3次,若至少摸到两个红球就中奖,否则无奖;B方案是:从装有3个红色小球和7个白色小球的箱子里每次摸1个小球,有放回地摸3次,若至少有两次摸到红球就中奖,否则无奖;其中箱子里的小球除颜色和编号外完全相同.(Ⅰ)若某顾客用A方案抽奖一次,求他抽到的3个小球中红球个数X的分布列和期望;
(Ⅱ)若甲、乙两顾客分别用A、B方案各抽奖一次,它们中奖的概率是否相同?若你去抽奖,将选择哪种方案?说明理由.
分析 (1)X可取0,1,2,3,且服从超几何分布,分别求出相应的概率,由此能求出X的分布列和期望EX.
(2)设甲、乙各抽奖一次,中奖的事件分别为C、D,分别求出P(C)和P(D),由此能求出结果.
解答 (本小题满分12分)
解:(1)X可取0,1,2,3,且服从超几何分布,
P(X=0)=$\frac{{C}_{7}^{3}}{{C}_{10}^{3}}$=$\frac{7}{24}$,
P(X=1)=$\frac{{C}_{3}^{1}{C}_{7}^{2}}{{C}_{10}^{3}}$=$\frac{21}{40}$,
P(X=2)=$\frac{{C}_{3}^{2}{C}_{7}^{1}}{{C}_{10}^{3}}$=$\frac{7}{40}$,
P(X=3)=$\frac{{C}_{3}^{3}}{{C}_{10}^{3}}$=$\frac{1}{120}$,…(4分)
∴X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{7}{24}$ | $\frac{21}{40}$ | $\frac{7}{40}$ | $\frac{1}{120}$ |
(2)设甲、乙各抽奖一次,中奖的事件分别为C、D,则
由(1)知P(C)=$\frac{7}{40}$+$\frac{1}{120}$=$\frac{11}{60}$,…(8分)
乙按B方案抽,P(D)=${C}_{3}^{2}•0.{3}^{2}×0.7+{C}_{3}^{3}•0.{3}^{3}$=$\frac{27}{125}$.…(10分)
甲、乙中奖的概率不相同,
∵$\frac{27}{125}>\frac{11}{60}$,∴P(D)>P(C),
∴应选择B方案抽奖. …(12分)
点评 本题考查概率的求法及应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
6.y=sin2x的图象是由函数y=sin(2x+$\frac{π}{3}$)的图象向( )个单位而得到.
| A. | 左平移$\frac{π}{12}$ | B. | 左平移$\frac{π}{6}$ | C. | 右平移$\frac{π}{12}$ | D. | 右平移$\frac{π}{6}$ |
16.已知函数f(x)=ax3-x2+4x+3,若在区间[-2,1]上,f(x)≥0恒成立,则a的取值范围是( )
| A. | [-6,-2] | B. | $[-6,-\frac{9}{8}]$ | C. | [-5,-3] | D. | [-4,-3] |
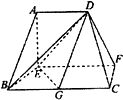 在如图所示的多面体中,底面BCFE是梯形,EF∥BC,EF⊥EB,又平面ABE⊥平面BCFE,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$.
在如图所示的多面体中,底面BCFE是梯形,EF∥BC,EF⊥EB,又平面ABE⊥平面BCFE,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$.