题目内容
14.下列各组函数是同一函数的是( )| A. | y=$\frac{2x}{x}$与y=2 | B. | y=$\sqrt{{x}^{2}}$与y=($\sqrt{x}$)2 | C. | y=lgx2与y=2lgx | D. | y=$\frac{{x}^{2}}{x}$与y=x(x≠0) |
分析 由定义域相同,对应关系相同,是同一函数,依次判断可知A,B,C均不是,D为同一函数.
解答 解:对于A,y=$\frac{2x}{x}$=2(x≠0)与y=2,定义域不同,不是同一函数;
对于B,y=$\sqrt{{x}^{2}}$=|x|,与y=($\sqrt{x}$)2=x,(x≥0)定义域不同,对应关系不同,不是同一函数;
对于C,y=lgx2与y=2lgx,前者定义域为{x|x≠0},后者定义域为{x|x>0},不是同一函数;
对于D,y=$\frac{{x}^{2}}{x}$=x(x≠0)与y=x(x≠0),定义域相同,对应关系相同,是同一函数.
故选:D.
点评 本题考查同一函数的判断,只要定义域相同,对应关系相同,就是同一函数,属于基础题.

练习册系列答案
相关题目
9.函数f(x)=$\left\{\begin{array}{l}{2^{-x}}-1,x≤0\\{x^{\frac{1}{2}}},x>0\end{array}$满足f(x)=1的x值为( )
| A. | 1 | B. | -1 | C. | 1或-2 | D. | 1或-1 |
19.偶函数f(x)在[0,+∞)上单调递增,若f(1)=0,则不等式f(x)>0的解集是( )
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(1,+∞) |
6.y=sin2x的图象是由函数y=sin(2x+$\frac{π}{3}$)的图象向( )个单位而得到.
| A. | 左平移$\frac{π}{12}$ | B. | 左平移$\frac{π}{6}$ | C. | 右平移$\frac{π}{12}$ | D. | 右平移$\frac{π}{6}$ |
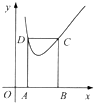 如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.
如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.